Formules, differentiaalvergelijkingen, toepassingen, deel 2 Het tweede artikel over de toepassingen van differentiaalvergelijkingen
introduceert een nieuw soort oplossingsmethode: de numerieke oplossingen. Deze zijn tegenwoordige
belangrijker dan die gebruikt bij de beschrijving van de trillende veer, wat
heet een "analytische oplossing".De numerieke oplossingsmethode maakt het mogelijk ook ingewikkeldere differentiaalvergelijkingen op te lossen, horende bij situaties in de natuur ingewikkelder dan het simpele geval van zwaartekracht versus veerkracht. Het eerste voorbeeld voor ingewikkeldere situaties is toch redelijk simpel gehouden, en is het bekende "vossen en konijnen"-model  , staande voor de algemene situatie van
twee diersoorten in interactie: een roofdier en een prooidier.In een redelijk beperkte ruimte, zeg een duingebied, loopt een aantal konijnen en een aantal vossen rond, en de vossen eten konijnen voor hun exclusieve levensonderhoud. En als er genoeg konijnen zijn, krijgen de vossen veel jongen, die tezamen steeds meer konijnen gaan eten. Tot het punt bereikt is dat er een tekort ontstaat aan konijnen. Dan beginnen de vossen met uitsterven, en als er genoeg gestorven zijn, hebben de konijnen weer genoeg ruimte om nieuwe konijnen te kweken, enzovoort. Hier zijn de bijbehorende vergelijkingen, met de konijnen als \( x \) en de vossen als \( y \) :
In de uitwerking zijn de constanten wat anders gedefinieerd, om ze directer te laten aansluiten op het menselijke begrip. Nodig zijn de volgende constanten, tezamen met hun waarde gegeven in het model (dit model en computerprogramma komen van hier
):
Nu zijn de vergelijkingen nodig die laten zien hoe de aantallen veranderen. Daartoe wordt, voor de numerieke oplossingsmethode, de differentiaalvergelijking met zijn oneindig kleine verschillen weer teruggebracht op zijn wereldlijke pootjes door de verschillen eindig groot te maken. Wat in dit soort vergelijkingen gedaan wordt door simpelweg de tijd in stukjes te hakken, en voor de aantallen gedurende die stukjes tijd te veronderstellen dat ze constant zijn. Fout, natuurlijk, maar de clou is om de stukjes zodanig klein te kiezen dat de fout klein (genoeg) is. In dit geval zijn de stukjes periodes van een kwart jaar. De standaardperiode van het model is 100 jaar. Eerst bereken je de veranderingen per stukje:
En dan de nieuwe aantallen:
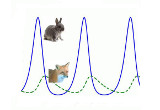
En doe dit voor alle stapjes tussen ingestelde begin- en eindtijd (deze reeks vergelijkingen tezamen is het equivalent van de oorspronkelijke differentiaalvergelijking, maar dan voor eindige stapjes - het heet een "differentievergelijking") Hier is het resultaat: Het resultaat dat je zou verwachten: golfbewegingen. En dit plaatje is niet een statische illustratie in de vorm van een jpg of gif, maar de directe weergave van de berekening uitgevoerd door het model. Voor hen die dit niet geloven of met het model willen spelen: er staat een interactieve versie hier  .Wat die interactieve versie ook laat zien dat de vorm van de golfbewegingen afhangt van de diverse parameters, de een sterker dan de andere. Op die manier is weer veel extra te leren van de dynamiek van het systeem. De numerieke behandeling is dus een vruchtbare methode voor verder onderzoek. Naar Evolutie 
, of
site home
 .
|