Uitwerking bij Abstractieladder: ordenen
 Het
schematische voorbeeld van de abstractieladder
 laat zien dat het
abstractieproces niet iets is dat gaat volgens vaststaande regels, in de
zin: van regels die altijd van toepassing zijn. De keuze tussen ordenen op
kleur of ordenen op vorm, en dat dan weer het aantal hoeken, is er eentje die je intuïtief
maar niet beredeneerd kan maken - althans: niet dusdanig beredeneerd dat je
de alternatieven kan uitsluiten.
Twee extremen van dit spectrum zijn
bekend, zij het natuurlijk niet in deze toepassing. Het ene extreem is hoe
het leren van meer basale dingen gaat. Theorie op schrift ervan kent deze
redactie, maar dit filmpje
 op YouTube legt het glashelder uit. De context
is die van het worden van een expert op een bepaald terrein. Startpunt is
het bekende adagium van de wetenschapsjournalist Malcom Gladwell, dat voor
het bereiken van expertdom tienduizend uren oefening nodig zijn, en of dat
klopt.
Hiervoor lijken vooral twee velden in aanmerking te komen:
velden waarop bijna tot in het oneindige tot verbetering lijkt te leiden,
voornamelijk in de sport, en velden waarop een sterke verbetering in
diepgang mogelijk lijkt, voornamelijk in de natuurwetenschap en de
wiskunde.
Het sportvoorbeeld laat meteen beperkingen zien voor het
criterium, want waar voor iedereen geldt dat oefening leidt tot vooruitgang,
gaat bij sommigen de vooruitgang sneller en/of verder dan bij anderen.
Dat heet sporttechnisch "oefenbaarheid", en in de volksmond "talent".
En bij de diepgang-gevallen lijkt hetzelfde aan de hand - dat noemt men
dan ook wel slimheid of intelligentie.
Maar het filmpje noemt een tweede factor
voor de effectiviteit van het proces: terugkoppeling. De sporter krijgt die
terugkoppeling meestal automatisch: de bal gaat in of uit, en dergelijke. De
functie van een coach is te zorgen voor extra terugkoppeling.
Maar
die situatie heeft tegenvoorbeelden die wijzen op nog een factor, met als
eerste voorbeeld het roulettespel. De roulettespeler krijgt herhaalde
keiharde terugkoppeling, winst of verlies, maar bereikt niets dat in de
buurt komt van het zijn van expert: hij is en blijft een gokker.
En
wel omdat de omgeving, het roulettespel en het roulettewiel, niets anders
produceert dan willekeur.
Dus de omgeving moet niet alleen
terugkoppeling bieden, die omgeving moet ook een achterliggende regelmaat
hebben, of zoals het filmpje het uitdrukt: "valide zijn".
En hier
hebben we dus de connectie met het model van de abstractieladder: het
criterium dat je kiest bepaalt de leuze van aspect in de achtergrond wat men
gebruikt als terugkoppeling, en sommige keuzes zijn meer "valide", kom je
verder mee, dan
andere.
En dat merk je niet vooraf, en dat weet je niet vooraf, maar
dat merk je door diverse keuzes te proberen.
Het vraagteken in het
schema.
Het filmpje geeft
krasse voorbeelden van velden waarin men het idee van expert hoog houdt,
onder de noemer "deskundige", maar de Amerikaanse naam voor deze vormen van
deskundigen, "pundits", geeft al aan dat ze niet in te hoog aanzien
staan. Voor het geval van politieke of economische analisten blijkt dat de
deskundigen slechter presteren dan door volkomen willekeurige keuzes te
maken. De oorzaak wordt niet genoemd, maar kan met hoge aannemelijkheid
worden vastgepind aan de invloed van emoties.
Uit de eis van de
validiteit van de omgeving, zou men de conclusie kunnen trekken dat we ons
dan maar zo veel mogelijk moesten beperken tot omgevingen waarvan de
validiteit vast staat, in het gebruikte voorbeeldmodel dat van de vorm van
de driehoeken, wat officieel heet "geometrie", wat een deelgebied is van de
wiskunde. Laten we alles herleiden tot wiskunde. Dat leidt tot meer
zekerheid
Daarover kwam op
dezelfde dag een filmpje op YouTube onder ogen, over de paradox van Russell
, ontdekt door de wiskundige en filosoof Bertrand
Russell in 1901.
Wat begint met het streven van wiskundigen om een definitieve definitie
te komen van het begrip "getal". Wat hebben "één", "twee", "drie",
enzovoort gemeen?
Wat je kan zien als de punt van de piramide van de
abstractieladder, als je aanneemt dat alles bij elkaar genomen kan worden in
één ladder.
Waarbij men begint met de verzamelingenleer, omdat dat
hetgeen is wat een getal is: het doet er niet meer toe wat de dingen zijn,
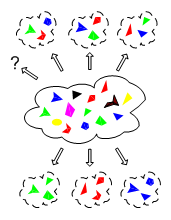
we nemen ze bij elkaar en tellen alleen het aantal. De "verzameling" is in
het diagram van de abstractieladder de wolkachtige stippellijnen rond de
objecten.
Het filmpje toont snel alle stappen die direct lijken te
volgen uit die eerste definitie: je mag alles insluiten in een verzameling.
Ook verzamelingen. Wat al meteen een vorm van cirkel is. En dus ook een vorm
van terugkoppeling.
Maar dat gaat dus mis. Wat begint met zaken als
"de verzameling van alle verzamelingen". En mis is, zodra je op één of
andere manier een negatie introduceert; een "negatie" zijnde een minteken,
een ontkenning, en dergelijke. Wat allemaal allang bekend was als "De Kretenzer
die stelt dat alle Kretenzers liegen".
Een cirkel, de
Kretenzer heeft het ook over zichzelf, in combinatie met een negatie:
"liegen" is "niet de waarheid spreken".
Wat dan via de keten van gevolgtrekkingen terugkomt bij de
definitie van verzameling: je mag kennelijk dus niet alles toelaten tot een
verzameling.
Maar dan gaat je definitie van "getal" als aangevende
alleen "aantal" los van iedere inhoud de mist in.
De twee beschreven
processen vergelijkende: het "expert worden" en het "exact beschrijven",
laat een opvallende dubbelrol van het proces van terugkoppeling zien: in het
praktische "expert worden"-geval blijkt het een noodzakelijke factor, en in
het "exact beschrijvende" blijkt het een definitief verstorende factor.
En er zijn meer raakvlakken tussen de twee situaties. De persoon die
informatie verschaft die de werkelijkheid tegenspreekt, kan gezien worden
als de overtreffende trap van een "niet-valide omgeving": niet alleen
willekeur, mar regelrechte tegenspraak.
En de auteur van het
Russell-filmpje verschaft een ander raakvlak, met zijn stelling dat de
paradox er eigenlijk eentje is die geformuleerd moet worden in termen van "predication",
de actieve vorm van het gebruiken van een "predicate", wat vertaalt
als: "things said about an object". Het door de auteur gebruikte
voorbeeld: "Garfield is a cat".
En daar zit je meteen midden
in de abstractieladder.
Want "Garfield is a cat" is in vorm
identiek aan "Bessie is a cow", het archetypische voorbeeld waarmee
de abstractieladder begint, in de versie van Hayakawa.
Waarmee ook
direct duidelijk is dat er een verband is met de "expert worden"-situatie:
zowel "... is a cat" als "... is a cow" zijn de resultaten
van vele ervaringen met een valide omgeving. Heb je na een paar keer door
dat je dat grote zwart-witte beest kan gebruiken om te melken, en je ziet
nog zo'n groot zwart-wit beest, dan blijkt dat je dat meestal tot vrijwel
altijd ook kan melken.
De tennisser wordt getraind in het hanteren
van een tennisracket, en het kind wordt getraind in het hanteren van woorden
en taal.
Enzovoort.
Door middel van terugkoppeling.
De terugkoppeling ontbreekt in de weergave van de abtractieladder in de
versie van Hayakawa:
Het is een lineair model (in het boek als geheel staat uitleg die wel
op terugkoppeling neerkomt). Dat is niet het geval voor de originele versie
van Korzybski:
Links in één van zijn originele modellen, waarin de parabool boven de
fysische wereld voorstelt (origineel: microscopische deeltjes), de cirkels
eronder de door de mens waargenomen objecten, en de reeks rechthoekjes de
verschillende niveaus van "labels" die de mens erop plakt. Dat laatste zijnde het
proces van abstraheren.
De terugkoppeling links is wat
verwarrend in dat het proces van abstraheren qua oriëntatie weer omhoog
gaat, tegen de in gedachten continue lijn van "steeds abstracter is steeds
verder weg van de werkelijkheid" in. In het schema rechts is dat ondervangen
door de terugkoppeling alleen procesmatig weer te geven middels de pijl naar
boven.
Een derde representatie van terugkoppeling door Korzybski
is terug te vinden in zijn verbaal uitgesproken uitleg, zie bijvoorbeeld
hier
.
Wat in het schema wordt als dit:
Korzybski herhaalt aan het einde de cruciale observatie hierin: het gaat
door 'indefinitely'. Wat een synoniem is van het wiskundige begrip
"infinitely".
En in de wiskunde is een proces, een operatie,
die uitkomt op "infinite", "oneindig", een teken dat er iets fout
is gegaan.
Een risico dat onlosmakelijk verbonden is aan
terugkoppeling, zijnde een cirkelproces, zijnde iets dat zich onbeperkt
herhaalt.
Iets dat bekend is sinds de oudheid:
Hier in de vorm van de "ouroboros".
In computertalen, volgens standaardopvattingen een vorm
van wiskunde, moet een terugkoppeling, een "loop", altijd voorzien worden van een
voorwaarde voor beëindiging ervan. Doe je dat niet, genereert het
computer-vertaalsysteem (de "compiler") een foutmelding, en heeft de
compiler die optie niet, loopt de computer vast en moet je hem herstarten.
Als Korzybski deze ontwikkeling had meegemaakt, had hij verwezen
naar de noodzaak voor het menselijke denken om hun systeem te herstarten,
want dat is hetgeen hij met bijna zoveel woorden schrijft in de inleiding
van zijn magnum opus: Science and sanity
 .
Een ander ding dat hij gedaan had, was
verwijzen naar de actieve rol van de neurologie in dit proces, want dat is
hetgeen hij in Science and sanity een groot deel van de aandacht aan
besteedt.
De ontwikkeling van de kennis van de neurologie is één van
de belangrijkste ontwikkelingen sinds de tijd van Korzybski. In Science
and sanity probeert hij de denkprocessen te modelleren aan de hand van
de werking van losse neuronen, terwijl inmiddels duidelijk is dat dit
gebeurt in collectief gedrag van grote groepen van neuronen.
En daarin
ligt een groot onderscheid tussen de twee aspecten van "leren door ervaring
en terugkoppeling": het leren van fysieke vaardigheden als in de sport,
eigenlijk alleen door heel veel oefening, gebeurt op een andere plaats in
het brein dan door het proces van groeperen en abstraheren van de
abstractieladder.
Dat laatste vindt plaats, zoals beschreven in Abstractieladder, kort
, in de hippocampus en aanpalende onderdelen van de cortex, het eerste in
kleine hersenen of cerebellum - voor meer anatomisch detail zie het
interactieve Neurologie, overzicht
 . Het cerebellum is een onderdeel van de hersenstam, en heeft
een veel simpelere structuur dan de rest van het brein erboven, met de
emoties en abstracties. Het doet voornamelijk aan zeer veel opslag, wat
eruit blijkt dat het de helft van de neuronen van het brein bevat, met
daarin een beetje terugkoppeling waarvan men wel de elementen, de specifieke
soorten neuronen, kan aanwijzen, maar onduidelijk is hoe het werkt. Maar qua
structuur allemaal precies overeenkomende met wat je in de praktijk ziet bij
mensen die hun lichamelijke vaardigheden oefenen.
Dat laatst deels
ook geldende voor de werking van de hippocampus en omgeving, want in de
diagrammen die men daarvan tekent zie je ook voortdurend cirkelvormige
processen, zie de volgende doorsnede van de hippocampus (Wikipedia.org,
opgeslagen 09-02-2023,
):
Je mag zelfs aannemen dat de om elkaar heen-liggende spiraalvormige
structuur van het geheel ontstaan is om de terugkoppelingspaden tussen de
verschillende lagen zo kort mogelijk te houden (in de evolutie is snelheid
een zeer groot voordeel).
De natuur oftewel de evolutie voorziet de
cirkelprocessen automatisch van een beperkende factor: wat dat niet heeft,
raakt in een cirkel, bevriest, is kwetsbaar, en gaat dood. De "denkende"
mens gaat het proces vertalen in symbolen, die die automatisch beperkende
factor niet hebben.
Dat gaat dus fout. Regelmatig.
Russell
kwam op zijn paradox bij het bestuderen van het werk van Gottlob Frege
,
een of de grondlegger van de theorie van verzamelingen, bedoeld om nu eens
precies te beschrijven wat een getal is. Wta is dat: "vier" ... ???
Een andere YouTube-filmer dan de
eerder genoemde ( , na 7:32 min.), "roept vertwijfeld": "Ik probeerde zelf te formuleren
wat een getal is maar moest voortdurend de term zelf gebruiken".
Het
lijkt allemaal toch sprekend op wat Hayakawa citeert van Wendell Johnson,
samengevat in "Chasing each other in verbal circles"
, of:
Het is natuurlijk mogelijk dat hier een oplossing voor is ("axiomatic
set theory" of "Zermalo set theory"
) maar die zullen vermoedelijk weinig praktisch
zijn. Wel praktisch is de oplossing die Hayakawa aandraagt:
Iets dat, als je het somber wilt zien, eigenlijk alleen binnen de
natuurwetenschap
...
... begrepen wordt.
Iets dat Korzybski uitstekend begreep, gezien
zijn voornemen in de inleiding van Science and Sanity om de
menswetenschappen te hervormen naar het model van de natuurwetenschappen.
En iets waar de huidige menswetenschappers en hun aanhang in het
maatschappelijke debat zich ten sterkste tegen verzet, onder het hanteren
van de term "sociaal darwinisme"
, voor de wetenschappelijke vorm van
menswetenschappen.
De aanhangers van het gebruik van de term "sociaal
darwinsime", in het maatschappelijke debat aan te duiden als "de
politieke-correctheid", hebben wél precieze definities.
Natuurlijk
niet van "getal", maar van begrippen als "Vrijheid", "Gelijkheid",
"Mensenrechten", enzovoort.
Wat, zoals Hayakawa uitvoerig uitlegt, in de
praktijk natuurlijk allemaal ...
... is.
Maar zoals de historische uitvinders van de Precieze
Definities, de auteurs van Het Oude Testament, uitvoerig aangetoond hebben:
het onderhouden van Precieze Defnities is een uiterst besmettelijk
verschijnsel.
Maar ook daarvan is, door de voortgang van de
neurowetenschappen, inmiddels bekend hoe het werkt: het elkaar bevestigen in
het bestaan van Precieze Definities maakt in de breinen van de betrokkenen
extra dopamine vrij
.
En het vrijmaken van extra dopamine is de bron
van alle verslavingen.
En dat het echte verslavingen zijn, valt af te
lezen uit hun reacties op tegenspraak: van scheldpartijen
tot vervolging
.
En dat het echte puur emotionele
neurologische processen zijn, valt op wat hoger niveau af te lezen uit de
eerste reactie van Gottlob Frege, een uiterst redelijk man, op de brief van
Russell waarin deze de vraag inhoudende zijn paradox stelde: hij stortte in
en werd dusdanig ziek dat hij naar het ziekenhuis moest.
Deze
verschijnselen zijn allemaal het gevolg van het vrijkomen van andere
neurotransmitters dan dopamine, vermoedelijk de combinatie van noradrenaline
("stress") en acetylcholine ("afkeer", "walging").
Maar het geval van
de persoon van Frege leidt naar nog een vorm van cirkel of terugkoppeling.
Als je slechts een korte samenvatting van zijn leven leest, is onmiddellijk
duidelijk dat hij sterk gedreven was in het brengen van eenvoud en regelmaat
in de wiskunde. Dat wil zeggen: in het omhoog klimmen op dat deel van de
ladder van abstracties die zich afspeelt in de wiskunde. En het bereiken van
een stap op de abstractieladder is een operatie die plaats vindt in het
brein, en daar extra dopamine vrijmaakt. Zijn ineenstorting na het ontvangen
van Russell's brief heeft vermoedelijk in aanzienlijke mate te maken dat hij
juist op dat moment op extra hoge dopamine-niveaus zat bij het voltooien van
zijn theorie en boek.
Frege herstelde, en publiceerde zijn theorie en
boek voorzien van een appendix die het gebeuren beschreef, inclusief zijn
intellectuele schok: dat zijn aanpak tot contradictie leidde.
Dat
werd en wordt gezien als een negatieve uitkomst, maar dat hoeft het niet te
zijn. De juistheid van een methode van argumentatie heeft geen één-op-één
verband met de juistheid van de uitkomst: een argumentatie kan juist zijn en
de uitkomst niet (één van de premissen of waarnemingen vooraf klopt niet),
en een argumentatie kan onjuist zijn en de uitkomst juist - zoals in het
gezegde van Goethe: "Je hoeft niet in China geweest te zijn om te weten dat
de lucht daar ook blauw is".
Wiskundig gezien is die argumentatie
onbewijsbaar en mogelijk/vermoedelijk onjuist, maar in de werkelijkheid
klopt ze als een bus.
En de systematiek van Frege die tot een
contradictie leidt, heeft, op hoger niveau, vermoedelijk precies evenveel
waarde als systematiek die niet tot een contradictie leidt.
In beide gevallen wordt het oneindige veld van mogelijkheden van de
werkelijkheid en het beschrijven van de werkelijkheid verder ingevuld.
Wat Frege heeft laten zien, is dat je met recht-toe-recht-aan
methodieken niet overal komt.
Mogelijk moet er een methodiek van
circulaire vormen van aanpak komen.
Waarvan er sinds de tijd van
Frege al diverse instanties zijn ontdekt: cybernetica, chaostheorie,
enzovoort.
Ondertussen lijkt zowel het mislukken van Frege met het
definiëren van "getal" als het "indefinitely" van Korzybski te wijzen op een
fundamenteel probleem voor het hanteren van begrippen in het algemeen.
Dat is niet zo in de praktijk.
In de praktijk zijn er minstens
twee manieren waarop de cirkel doorbroken kan worden: je hebt in de praktijk
van een cirkel vaak niet de hele cirkel nodig. Een deel kan volstaan. Uit
Hayakawa
: "Wat is rood?" "Rood is een kleur!" "Wat is
kleur?", enzovoort.
Je kan de cirkel afbreken door na "rood" of na
"kleur" te wijzen op een groep dingen uit de werkelijkheid die daadwerkelijk
voldoen aan het criterium dat zit achter "rood" of "kleur".
Oftewel:
In de praktijk kan je vaak volstaan met stukjes cirkel en die behandelen als
een rechte lijn.
De tweede mogelijkheid van het doorbreken van de
cirkel is die van de faseovergang. Doordat steeds meer entiteiten bij de
cirkel betrokken worden, kan in de praktijk er met die entiteiten dingen
gebeuren die het cirkelproces verstoren of anderszins ongeldig maken. Het
simpelst zie je dat bij de abstractieladder van Hayakawa: zodra je van
koeien, dat wil zeggen het melkproducerend ding, overstapt op "vee", waarin
ook de stieren meedoen, kunnen er tussen de koeien en stieren dingen
gebeuren die je begrip van "aantal" als vaste factor onderuit halen.
In de praktijk zal je met deze factoren rekening moeten houden, en is de
vraag naar het bestaan van zuivere definities dus eigenlijk irrelevant.
Wat in versterkte mate geldt voor wetenschappelijke vakgebieden als de
sociologie, waar over het meest fundamentele aspect ervan: de "groep van
mensen"
, nog een richtingenstrijd aan de gang is, met richtingen uiteenlopend tot
het extreem dat er überhaupt geen "groepen van mensen" bestaan want "Ieder
mens is een individu". En waarin het in de werkelijkheid waarneembare
proces, de evolutie van de soort "mens" als de evolutie van "groepen van
mensen", gezien wordt als extreem dat sterk negatief beoordeeld wordt als
"sociaal darwinisme"
.
Voor de sociologie zal het
noodzakelijk zijn regels te ontwikkelen voor begrippen die niet herleidbaar
zijn dat "ja" versus "nee" of "waar" versus "onwaar" enzovoort, maar die een
ingebouwde onzekerheidsfactor hebben: wat natuurkundigen zeggen met
"Het is tussen 62 en 72", oftewel "Het is 67 plus of min 5", oftewel
"67 ± 5" . Het rekenen daarmee in meerdere stappen houdt op een gegeven moment
automatisch op, omdat de onzekerheden in iedere extra stap optellen, en de
totale onzekerheid op een gegeven moment de waarde van het gemiddelde
overschrijdt.
En tot slot een slot zoals het hoort: een filosofisch
slotwoord. Aan het einde van de reeksen vragen zoals "Wat is een getal?"
staat een vraag waar deze redactie aan herinnerd werd door een ander
YouTube-filmpje
, met de titel "How do you know that you know what you
know?". Overduidelijk een circulaire vraag, dus een vruchtbare bron
voor filosofen om over te filosoferen., wat ze inderdaad gedaan hebben sinds
de Oude Grieken en daarvoor.
En natuurlijk komen ook vele andere
concepten voorbij, zoals "waarheid".
In de loop van het verhaal van
de jongedame komt zelfs de oplossing als boven gegeven langs, voor deze
gelegenheid verder afgekort tot: "Als het werkt".
Het samen nemen van
een giraffe, een auto, een bloemkool en een schaar is mogelijk, en kan
voorgesteld worden met het getal "vier". Maar wat levert het je op? Of
iemand anders?
Niets.
Dat is wat het eerste filmpje bedoelt
met "validiteit": als je door ervaring, of statistische methodieken,
probeert te leren van iets waar geen regelmaat in zit, leert je niets.
En de troost is dat ondanks het feit dat je niet of misschien zelfs nooit zeker
lijkt te kunnen weten wat je weet, je door proberen en doorzetten zo
veel te weten kan komen, dat daar voor voorzienbare tijdschalen geen einde aan
lijkt te komen.
Addendum
In het laatste filmpje wordt gewag gemaakt van "Het
Gettier Probleem", slaande op een meneer die "ontdekt" heeft dat de
redelijke definitie van waarheid niet kan kloppen omdat er ook gevallen zijn
dat iets waar blijkt dat niet voldoet aan "de redelijke definitie" met als
voorbeeld een geit met veel haar die op een schaap lijkt. Enzovoort.
Goh ...
Gelukkig wordt ook vermeld dat zoiets al is eerder bedacht
door filosoferende woestijnbewoners die een wat donkerachtige wolk in de
verte zien en dan denken dat het rook is terwijl het in werkelijkheid een
zwerm insecten is.
Deze filosofen hebben dus ontdekt dat er gevallen
zijn die wel vallen onder hun definitie, maar dat niet doen
vanwege hun definitie.
Gunst ...
Daarom hebben de
verzamelingswolkjes in de uitgewerkte abstractieladder ook geen
doorgetrokken lijntjes, maar streeplijnen.
Omdat de grenzen niet
volkomen vast liggen.
En "niet volkomen vast liggen" betekent twee
dingen: dat er gevallen zijn die er toevallig buiten liggen maar er
wel toe behoren, en dat er gevallen binnen liggen zijn die er
volgens de definitie niet toe behoren.
We gaan
het niet bewijzen maar het vermoeden is dat als één van deze twee niet waar
is, het ook voor de ander geldt.
En als het zo is dat wat voldoet aan
de definitie dan ook zeker binnen de verzameling ligt, heb je dus een
absolute waarheid.
Een logisch zuivere definitie van de term "getal".
Wat nog maar eens ten overvloede laat zien waar al dit gefilosofeer
vandaan komt: de behoefte van woestijnbewoners naar wat zekerheid in het
leven.
Andere woestijnbewoners voelden die behoefte ook, en hebben
dat opgeschreven in een dik boek genaamd Het Oude Testament.
Van de
dingen die daarin staan, heeft de wereld nog steeds een ongelofelijke
hoeveelheid last, want de behoefte naar wat zekerheid blijkt een zeer
fundamenteel iets te zijn in het brein. Vraag maar aan meneer Frege.
Iets met dopamine, enzovoort.
Maar dat is dus een ander verhaal
.
Addendum 2
Dit tweede addendum is op dezelfde manier tot stand
gekomen als het eerste, en een groot deel van de hoofdtekst erboven: na het
noteren en het verwerken van het voorgaande.
Bij dit tweede addendum
zijnde de inval dat wat meneer Frege en deze auteur en iedereen anders
doet met dit soort activiteiten: zin heeft het dan en slechts dan (en dat in de
logische zin) als het ook overkomt bij andere mensen.
Wie wijs gaat worden in zijn eentje in een grot heeft hoogstens een invloed op de wormen
die zijn lichaam verteren.
Dat wil zeggen: er moet bij de ander op wie je jouw theorie over "Wat is een getal?"
wilt overbrengen als eerste al overeenstemming zijn over de allereerste stap:
het allereerste ding dat je in je verzameling gaat stoppen, en, zullen we maar meteen de volgende
stap meenemen: wat is eigenlijk een "ding"?
Met meteen ook maar het antwoord: "Een 'ding' is iets dat je kan aanwijzen".
Wat je hoogstwaarschijnlijk dus weer evolutionair moet benaderen: de menselijke communictie
is begonnen met aanwijzen:
De erbij geuite geluiden zijn natuurlijk volkomen willekeurig. Als je maar
voor hetzelfde ding elke keer dezelfde kreet gebruikt.
Wat dus geheel onbedoeld uitvoerig geïllustreerd wordt in het verzamelingen-filmpje,
waarin het als één van de aangewezen dingen gaat over "Lebron James", wat kennelijk
één of andere Amerikaanse sporter is ( we krijgen ook beelden), wat de autuer dus doet omdat hij
Amerikaan is en hij aanneemt dat iedere Amerikaan weet wat "Lebron James" is,
namelijk een mens die aan één of andere sport doet. En even vergeet dat hij
in een wijdere wereld leeft.
En dat geldt dus voor ALLE!!! andere dingen die zo terloops in verzamelingen
worden gestopt door mensen als Frege enzovoort: het zijn allemaal slechts kreten voor wat
ze aannemen dat iedereen weet dat ze ergens voor staan en waarvoor ze staan.
Of niet.
En als dat laatste het geval is, slaat het dus allemaal, het hele
bouwwerk, helemaal nergens op want je kan het niet testen want waar je het
over hebt bestaat niet.
Het is dan slechts een spelletje met symbolen - meestal donker gekleurde vlekjes
op een licht gekleurde achtergrond.
Zoiets als Conway's Game of Life
.
Je kan kan ook met je duimen gaan zitten draaien.
Kortom: ALLE begrippen die gebruikt worden eigenlijk zelfs voordat je begint
met je plannetje voor het definiëren van "getal", of iets dergelijks, zijn al ontstaan
in een schier oneindig complex bouwwerk gebouwd uit begrippen ontstaan door aanwijzen.
En er is in het vervolg van het bouwen aan dat bouwwerk dus veel voor
te zeggen om aan te nemen dat je je bouwwerk moet beperken tot begrippen die op enigerlei wijze zijn te herleiden
tot "aanwijzen".
Omdat "aanwijzen" uiteindelijk het enige is dat werkt om
een ander persoon te laten zien wat jij bedoelt met die primale
uiting die uiteen kan lopen van zeg de oerkreet "BOEWAHHH!!!" tot "1"
(spreek uit: "één", "one", "un", "uno", enzovoort).
Van welk laatste overigens allerwegen wordt aangenomen dat het
afstamt voor het symbool voor de eigen persoon:
In het Engels: "I".
Of, na het noteren van het voorgaande; om in ieder geval expliciet aan
te geven dat je nu een symbool gaat gebruiken voor iets dat je niet
kan aanwijzen in de werkelijkheid.
Zeg bijvoorbeeld: "Ik ga nu een
heel dik boek schrijven over iets dat niet bestaat ondat het oneindig groot
is".
Waarna je in dat boek, omdat het toch gaat over dingen die niet
bestaan, andere absurde dingen kan schrijven, zoals:
"Iedereen moet luisteren
naar wat ik zeg omdat ik een boek heb geschreven over iets dat oneindig
groot is, want dat is heel
knap van mij om een boek te schrijven over
iets dat oneindig groot is".
Kortom: deze verhandeling blijkt ineens
toch best wel interessante praktische kanten te hebben.
Terug naar Abstractieladder, kort
.
|
_600.png)
