|
De abstractieladder, deel 2 - beweeg over
de onderdelen voor uitleg - naar deel 1, 3
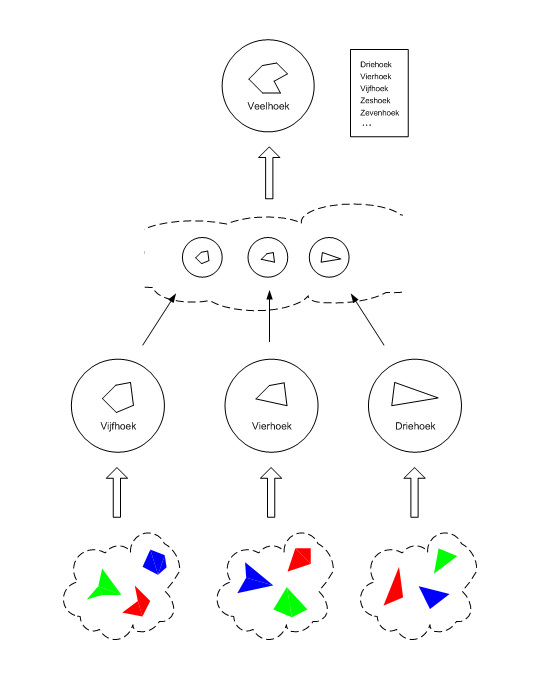
Groepering 2 van voorwerpen uit de werkelijkheid
Methode: Indeling naar aantal hoekpunten.
Aantal: vijf.
Groepering 2 van voorwerpen uit de werkelijkheid
Methode: Indeling naar aantal hoekpunten.
Aantal: vier.
Groepering 2 van voorwerpen uit de werkelijkheid
Methode: Indeling naar aantal hoekpunten.
Aantal: drie.
De wereld van de abstracties
Abstractieniveau 1.
Uit de groep van platte voorwerpen met de eigenschap dat ze vijf hoekpunten
hebben, wordt een gemeenschappelijke eigenschap gedistilleerd.
De gemeenschappelijke eigenschap van platte voorwerpen met vijf hoekpunten wordt
samengevat in een abstractie genaamd “vijfhoek”. Aan deze vijfhoek kunnen indien
gewenst dan weer de eigenschappen van een van de individuele voorwerpen gegeven
worden, dat wil zeggen: de ene vijfhoek staat voor allemaal. Dit is natuurlijk
een niet-bestaande vijfhoek, vandaar dat hij is aangegeven in een cirkel, en
zonder eigenschappen als kleur en dergelijke. Dit is een abstractie van het
eerste niveau.
De wereld van de abstracties
Abstractieniveau 1.
Uit de groep van platte voorwerpen met de eigenschap dat ze vier hoekpunten
hebben, wordt een gemeenschappelijke eigenschap gedistilleerd.
De gemeenschappelijke eigenschap van platte voorwerpen met vier hoekpunten wordt
samengevat in een abstractie genaamd “vierhoek”. Aan deze vierhoek kunnen indien
gewenst dan weer de eigenschappen van een van de individuele voorwerpen gegeven
worden, dat wil zeggen: de ene vierhoek staat voor allemaal. Dit is natuurlijk
een niet-bestaande vierhoek, vandaar dat hij is aangegeven in een cirkel, en
zonder eigenschappen als kleur en dergelijke. Dit is een abstractie van het
eerste niveau.
De wereld van de abstracties
Abstractieniveau 1.
Uit de groep van platte voorwerpen met de eigenschap dat ze drie hoekpunten
hebben, wordt een gemeenschappelijke eigenschap gedistilleerd.
De gemeenschappelijke eigenschap van platte voorwerpen met drie hoekpunten wordt
samengevat in een abstractie genaamd “driehoek”. Aan deze driehoek kunnen indien
gewenst dan weer de eigenschappen van een van de individuele voorwerpen gegeven
worden, dat wil zeggen: de ene driehoek staat voor allemaal. Dit is natuurlijk
een niet-bestaande driehoek, vandaar dat hij is aangegeven in een cirkel, en
zonder eigenschappen als kleur en dergelijke. Dit is een abstractie van het
eerste niveau, een abstractie direct afgeleid van de objecten van de werkelijke
wereld.
De wereld van de abstracties
Groepering 1 van abstracties op niveau 1.
Methode:
De abstractie tot driehoek kan ook gedaan worden voor voorwerpen met vier
hoekpunten tot een vierhoek, van voorwerpen met vijf hoekpunten tot een vijfhoek
enzovoort.
De driehoek, vierhoek, vijfhoek, enzovoort kunnen ook weer als individuen gezien
worden, waarvan men gemeenschappelijke eigenschappen kan zoeken.
De wereld van de abstracties
Abstractieniveau 2
De gemeenschappelijk eigenschappen van driehoek, vierhoek, vijfhoek, enzovoort
wordt samengevat tot de nieuwe abstractie “veelhoek”. Dit is een abstractie van
het tweede niveau: een abstractie van abstracties
| 