The abstraction builder |
"Herd" and "livestock" are generalizations of such an obvious nature, that it is hard to see them as abstractions al all. Yet they must have come into existence at some point in time, a time that for an individual person can be traced back to childhood, and the way children learn these things.
If growing up on a farm, by watching what daddy does when utterings the sounds "cow" and "cows". If necessary aided by some pointing of fingers.
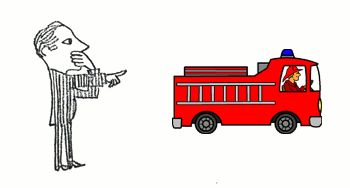
If growing up in the city, applicable to the familiar examples of "car" and "fire truck": if "car" and "red", then "fire truck"
(illustration using an idea taken from Hayakawa
).
So conclusion number one is: abstractions do not come into existence by themselves, but are acquired through experience. At least the more basic ones.
Which leads to the follow-up question: "How does the brain construct abstractions from experiences plus possibly some verbal input?"
This question seems more difficult to answer, if viewed from standpoint of language and its workings - one soon gets entangled in circular definitions. In the example given Hayakawa
: "What is red?". "Red is a color". "What is
color?". ... Etcetera.The solution lies in the alternative recipe for such situations given by general semantics: step down the ladder towards more concrete levels. The more concrete level invoked here is that of neurology, not in the usual sense of "neuro-pathology" but in the literal sense of "the laws of the nervous system".
When studying neurology while concentrating on what it is primarily for, which is the advancement of survival and reproduction, one soon learns that the building of abstactions may be not the only thing is meant for, but that it is surely one of the most essential aspects of it: the fish must know quite general characteristics of the preditor-fish, or else it is eaten by the first preditor that differs from the models it already has learned about. Leading to the conclusion that the knowledge it has about preditor-fish comes in the form of abstractions.
To be combined with our knowledge from biology that these processes can hardly be put in the same class as that of "human thinking". Leading to the conclusion that the construction of abstractions is not a human capacity, but one of animals in general. And at a very basic level at that, because fishes themselves are already quite basic, while it is clear that the argument can be continued for a quite a number of steps.
In this article, most of these steps are skipped, by noting that even at the level of the observation-system one can observe signs of the presence of a process of making abstractions. One of these lies in the knowledge of the process of the frog catching the speeding fly. The frog has only tiny fractions of seconds to react from the moment the fly comes into his field-of-view. He can achieve his catch because his eye is preprogrammed to detect movements, which it notices as movements of boundaries between light and dark. The signal the eye gives off on the passing of the fly is "fast moving boundaries between light and dark amounting to a dark spot". This signal is transmitted to the muscles with the least possible processing - etcetera.
Now it is well-known that the field of view of amost any kind of eye is build-up from individual light-sensitive cells, in nowadays terms: pixels
(link in Dutch, but the illustrations are clear enough) .
So the boundaries between light and dark are build up from lots of pixels, taking
corresponding aspects of them. In other words: these boundaries are
abstractions.So the "How?"-question pertaining to abstractions can be reduced to: "How does the eye build abstractions from pixels?"
To this question there exists a reasonable looking answer for quite some time now, which is called "Fast Fourier transformation" or FFT, or something that looks like FFT.
Fourier transformation
is the mathematical description of extracting from any repetative signal the
basic siganls it is build up from, where "basic" means signals having the
following shape:
|
Which it does by generating the entire range of basic signals or so much of it as is possible, and mixing them with the original signal, and looking if one gets any net result. You only get a net result when there are equal frequencies in both, according to a well-known phenomenon called "resonance", which is well-known because for example it made the Tacoma Narrows Bridge collaps
.So this is the basic method. But it cannot be used in nature, for our case of the eye, because it would take too much time, and nature cannot make analytical calculations anyway.
That is where the FFT-version of the process comes in. FFT hacks the signals into pieces, which is most effective for speed of one chooses multiples of eight. Secondly it takes for the repetative signal the most simple signal imaginable which has the form: 010101010101... etcetera. And thirdly, which is possible because of the previous two: the process of mixing can now be done using simple addition and subtraction. And these are operations nature indeed is able to perform. Neurons do this all the time. When a neuron fires because two of its neighbours have fired, it has performed an addition. When a neutron is inhibited from firing when his neighbour has fired, it has in fact performed a subtraction, because it has stopped the further transmission of the signal of his neighbour and its own - it has reduced these to zero.
Reproduced below is part of the explanation given elsewhere of how FTT works
, using these basic processes applied to a simple network
with logical gates representing neurons, having eight inputs to represent a signal, and eight
outputs to signify a possible regular pattern as an input signal. To speed
up the process a number of (regular) patterns have been predefined and one
irregular (number 5), besides
the possiblity to make your own by choosing "Free choice" (scroll down).
By clicking "Submit" one executes the FTT calculation according to the
scheme denoted by negative signs at the appropriate points, while at the
other points there are additions.
Warning: Undefined array key "ptr" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 222
Warning: Undefined array key "sch" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 223
Warning: Undefined array key "i01" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 311
Warning: Undefined array key "i02" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 312
Warning: Undefined array key "i03" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 313
Warning: Undefined array key "i04" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 314
Warning: Undefined array key "i05" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 315
Warning: Undefined array key "i06" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 316
Warning: Undefined array key "i07" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 317
Warning: Undefined array key "i08" in /home1/zweistrar/public_html/english/general_semantics/abstraction-ladder_diagram/abstraction-builder.php on line 318
As you will have noticed: the regular patterns do indeed produce a discriminating outcome: all outputs are zero except for one.
The reason that the more complicated process of Fourier transformation also works in this highly simplified case, is that the regalur patterns with which the input-signal is compared, is already build into the calculation-scheme, in this case being:
 |
Just follow the pattern of the location of the minus signs, and observe that it reflects the regular patterns in the input signal that it can identify with a signal on one specific output. Note that there are more patterns that give similar results, due to various symmetries.
In these examples the FFT processing pattern came into existence by human design. The relevant case is how they can develop in living organisms. This, of course, is through the process of evolution. For this to work, one only has to have a simple one-step by one-step path from basic functionality to more complicated ones, which sometimes is difficult to find, but for the example of the optical construction of the eye
itself has indeed be found
(link partly in Dutch, but the illustrations are clear enough). The fact
that neurons have connections with multiple neighbours by themselves and that
the FTT process involves only additions and subtractions, enables the
development towards the regularity required. The result can be observed in the case of the eye
(link in Dutch, but the illustrations are clear enough) - even on first glance one can recognize
the layered structure one also finds in the basic FTT-transformer, with neurons acting as the gates and their axons as connections.
It is the fact that this very fast real-time processing in the retina takes
place, that enables the frog to react almost instantaneously when a
fast-flying fly enters his field of view, and catch it with its tongue.This demonstrates the basic FFT process in a very simplified form. From which one can construct more detailed and complicated versions by adding additional numbers of inputs with corresponding secondary gates or neurons, and by having sequences of singular FFT transformators. All this without introducing any additional concepts.
That is, except for one. The FFT transformation as found in the eye came into existence by the process of evolution, and one can imagine that this applies to several more steps into the development of more complicated neural networks - the retina is of course an example of a neural network. However: at some point there must exist the possibility to adapt a neural network to own, real life, experiences of the individual organism - the process that more abstractly is called "learning". The addional concept that is required to make this happen is "feedback"
: the outcome of usage of the network is evaluated, and this evaluation is
used to adapt the structure of the network - the output is "fed back"
towards the network itself. "Learning" is nothing more than the adaption of
neural networks.With all this in mind, one can point at numerous parts of the nervous system that point to functionalities of neural networks. In the brainstem
(more illustrations in this
Dutch link
) this is the
"reticular formation"
, whose netlike appearence is probably due to two structures of layers
crossing each other.At the next major level of the brain, that of the basal ganglia and the limbic system, the most prominent example of a layered neural network is that associated with the hippocampus and associated areas. The hippocampus has been associated with the formation of memories for quite a long time, but recent research suggest at least an important secondary fucntionality. The first sign of this has reached the more popular media under the name of "the Jennifer Aniston neuron"
, a
neuron that fires when Jennifer Aniston (a portrait of, of course) came into
view, but later turned out to be a member of a family of similar neurons
associated with other persons. Subsequent and at the moment of writing (end 2014) recent research has shown that the hippocampus analyses the observational experience into abstract classes
of the kind:
human, female, blond, young, and stores these associated classes into memory
instead of the entire and complete observational experience. Where the term 'stores' doesn't
mean that the memories are stored in the
hippocampus, but that it sends the information towards the storage in this
form.These neurological abstract classed are, of course, the same as those of the abstraction ladder. Which should be read in that the known form of the abstraction ladder is an expresson in language-terms of the workings of the nervous systeem. Precisely the way the originator of general semantics, Alfred Korzybski
, imagined things to be. So the exact way the higher abstractions of the mind are formed is unkown at present. However, it is quite likely that this process has considerable similarities with the way simpler neural networks turn collections of millions of pixels into a much more limited number of contours. Etcetera.
