Generalisaties
 Generaliseren, oftewel: het onder één noemer trekken van op het eerste gezicht
verschillende zaken, is in ieder geval één van de belangrijkste denkmethodes,
zo niet de belangrijkste. Bijvoorbeeld voor een prooidier is het feit dat ieder
roofdier zijn eigen individuele kenmerken heeft totaal onbelangrijk - het enige
wat van belang is voor hem zijn de gezamenlijke - voor de antilope: geel-zwarte
strepen in de buurt (tijger): wegwezen. Generaliseren, oftewel: het onder één noemer trekken van op het eerste gezicht
verschillende zaken, is in ieder geval één van de belangrijkste denkmethodes,
zo niet de belangrijkste. Bijvoorbeeld voor een prooidier is het feit dat ieder
roofdier zijn eigen individuele kenmerken heeft totaal onbelangrijk - het enige
wat van belang is voor hem zijn de gezamenlijke - voor de antilope: geel-zwarte
strepen in de buurt (tijger): wegwezen.
Wat tevens laat zien hoe de capaciteit tot generaliseren zich evolutionair kan
ontwikkelen: wie het niet (goed) kan, overleeft niet.
Conclusie: generalisaties zijn een basaal onderdeel van
iedere vorm van aanleren. Tot bijna op het moleculaire niveau. Of preciezer:
vanaf het niveau waarop het mogelijk is ervaringen vast te leggen. En dat ligt
ruim voor bijvoorbeeld schaaldieren
 . .
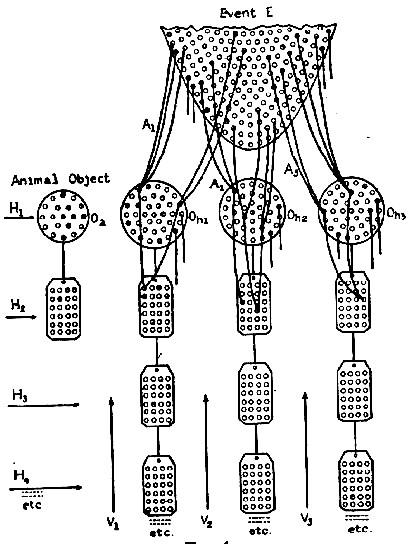 Dit
soort generalisaties zitten
dus ook diep in het menselijke systeem, maar zo diep, dat men van de meeste
ervan zich nauwelijks nog
bewust van is. Maar op de hoogste niveau van het menselijke denken, daar waar ze
min-of-meer nieuw zijn, vallen ze wel op, zij het meestal onder
andere termen. Voor zover bekend is de eerste systematische behandeling ervan
afkomstig van een pionier op het gebied van de betekenis van taal, Alfred Korzybski Dit
soort generalisaties zitten
dus ook diep in het menselijke systeem, maar zo diep, dat men van de meeste
ervan zich nauwelijks nog
bewust van is. Maar op de hoogste niveau van het menselijke denken, daar waar ze
min-of-meer nieuw zijn, vallen ze wel op, zij het meestal onder
andere termen. Voor zover bekend is de eerste systematische behandeling ervan
afkomstig van een pionier op het gebied van de betekenis van taal, Alfred Korzybski
 , gepubliceerd in het kader van een poging tot integratie van de
natuurwetenschappen en menswetenschappen onder de titel Science and Sanity
(1933). Zijn versie van de relatie tussen generalisaties noemde noemde hij de "structural
differential"
, gepubliceerd in het kader van een poging tot integratie van de
natuurwetenschappen en menswetenschappen onder de titel Science and Sanity
(1933). Zijn versie van de relatie tussen generalisaties noemde noemde hij de "structural
differential"
 , zie rechts.
, zie rechts.
 Het
werk van Korzybski was kennelijk te alomvattend om goed doorgegeven kunnen te
worden en het begrip "structural
differential" sloeg niet aan. Dat werd enigszins beter met de publicatie van
Language in Thought and Action (1949) van S.I. Hayakawa, die de "structural
differential" vereenvoudigde tot de "abstractieladder", waarbij "abstractie"
gewoon een andere term is voor generalisatie - zoals aangegeven door het door
Hayakawa geïntroduceerde archetypische voorbeeld: "Bessie de koe", "koeien",
"vee", "boerderijtoebehoren" enzovoort. Telkens worden de begrippen algemener (generaler),
en gaan meer specifieke eigenschappen verloren (abstracter). Het boek van
Hayakawa werd redelijk bekend en nog al eens gebruikt bij het vak der Algemene
taalwetenschappen. De abstractieladder heeft zijn voornaamste bekendheid in het
vak van "creatieve writing". Het
werk van Korzybski was kennelijk te alomvattend om goed doorgegeven kunnen te
worden en het begrip "structural
differential" sloeg niet aan. Dat werd enigszins beter met de publicatie van
Language in Thought and Action (1949) van S.I. Hayakawa, die de "structural
differential" vereenvoudigde tot de "abstractieladder", waarbij "abstractie"
gewoon een andere term is voor generalisatie - zoals aangegeven door het door
Hayakawa geïntroduceerde archetypische voorbeeld: "Bessie de koe", "koeien",
"vee", "boerderijtoebehoren" enzovoort. Telkens worden de begrippen algemener (generaler),
en gaan meer specifieke eigenschappen verloren (abstracter). Het boek van
Hayakawa werd redelijk bekend en nog al eens gebruikt bij het vak der Algemene
taalwetenschappen. De abstractieladder heeft zijn voornaamste bekendheid in het
vak van "creatieve writing".
Maar hoewel de abstractieladder van Hayakawa gemakkelijker is bij uitleg, is de
structural differential gedetailleerder en vollediger.
Zoals al door Korzybski opgemerkt, voert het waarnemingsapparaat
op automatische wijze al talloze generalisaties uit. Zo worden van de huid
van de koe niet de aparte moleculen waargenomen, maar alleen een zwart-wit-patroon
- als het een Friese koe is. Iets dat dus ook steeds verder gaat, maar dan de
diepte in. Oftewel: het waarnemingsveld is een scheidslijn van twee reeksen: de
hogere abstracties van het menselijke denken, en de lagere abstracties van het
menselijke waarnemen.
Dit laatste is een wijze van formuleren die uitgaat van een speciale positie van
de mens. Dat uitgangspunt heet in de filosofie of filosofie der
natuurwetenschappen "antropocentrisch", wat een slechte naam heeft omdat
daaronder ook vallen oude opvattingen als "De Aarde is het middelpunt van het
heelal", enzovoort, waarbij het in de geschiedenis van de wetenschappen telkens
zo was dat het antropocentrische uitgangspunt niet juist bleek.
Laat je het antropocentrisme ook hier vallen, dan is er niets anders dan één
continue reeks van generalisaties, vanuit het submicroscopische tot aan alles
overkoepelende concepten als "God" en "heelal". Met als voordeel dat algemene en
methodologische lessen geleerd op het ene niveau toegepast kunnen worden op
(alle) andere niveaus.
Een les uit de natuurkunde is de introductie van de terminologie van
veel-naar-één proces en zijn omgekeerde: één-naar-veel. Alle stappen op de
abstractieladder en generalisaties in het algemeen zijn veel-naar-één processen,
zoals door Hayakawa zelf aangegeven maar niet benoemd middels het aantal en de
soort van symbooltjes op het dienblad van het mannetje dat de ladder beklimt.
Het zwart-wit patroon van de koe is het resultaat van de reflectie van licht op
tienduizenden koeieharen en de verschillende manier waarop de reflecteren.
Zoals alle gegeven voorbeelden laten zien worden met generalisaties groepen
entiteiten bij elkaar genomen op grond van één of meerdere gezamenlijke
eigenschappen. Eén van de lessen uit de natuurkunde is dat zulke eigenschappen
nooit voorkomen in de vorm van "absoluut dit" versus "absoluut niet dit". Er is
hoogstens "heel erg veel dit" versus "ontzettend weinig dit", met een
continu verlopend overgangsgebied.
Het fysieke voorbeeld ter illustratie is het zogenaamde "Galton board",
zie hieronder (van hier
 ):
):
Deze knikkerbaan is bedacht door de statisticus Galton
 ter illustratie van de
zogenaamde binominale ("tweewaardige") verdeling, de mooie naam voor het proces
van achter elkaar een reeks "ja of nee" of "links of rechts" besluiten nemen op
willekeurige wijze, en dan kijken welke combinaties zoal voorkomen:
links-rechts-links-links- ... , rechts-rechts-links-links- ..., enzovoort. In
het knikkerboord valt of stuit de knikker van boven op de spijkertjes en valt naar links of rechts. ter illustratie van de
zogenaamde binominale ("tweewaardige") verdeling, de mooie naam voor het proces
van achter elkaar een reeks "ja of nee" of "links of rechts" besluiten nemen op
willekeurige wijze, en dan kijken welke combinaties zoal voorkomen:
links-rechts-links-links- ... , rechts-rechts-links-links- ..., enzovoort. In
het knikkerboord valt of stuit de knikker van boven op de spijkertjes en valt naar links of rechts.
Om dit goed te laten werken, moet de knikker precies boven het spijkertje worden
losgelaten, anders gaat hij altijd naar links of altijd naar rechts. Als je dit
proefmatig vaststelt door de loslaatplaats van het knikkertje van links naar
rechts te variëren, krijg je deze verdeling:
De les uit de natuurkunde is dat er altijd zo'n overgangsgebied is, met in met
midden een fifty-fifty kans. Voor alle eigenschappen dus ook voor de
eigenschappen die groepslidmaatschap bepalen. Dus voor alle generalisaties.
Deze vaagheden zouden een problemen kunnen vormen. In de natuurkunde is dit veel
minder het geval, omdat de meeste generalisaties zodanig zichzelf wijzen dat ze
nauwelijks als generalisaties worden gezien: de begrippen molecuul, atoom en
alles die kleinere kant op zou ook als individu kunnen worden gezien, maar er is
geen natuurkundige die het in zijn hoofd haalt om er als zodanig over te denken.
Veelal wordt expliciet het tegenovergestelde gesteld: moleculen, atoom, en
enzovoort heten dan "onderling verwisselbaar".
 Je
begint een overgangsgebied te raken zodra moleculen in vaste vorm komen. Hier
rechts staat een illustratie van sneeuwvlokken - overduidelijk allemaal met een
hoogst individuele structuur, en hier is op zicht al van toepassing: "Er is er
geen een hetzelfde".
Desalniettemin is het volkomen ongebruikelijk om sneeuwvlokken als individuen te
zien. Van individuele sneeuwvlokken telt voor zover het mensen betreft slechts
één enkele waarde: de hoeveelheid warmte die ze aan de omgeving onttrekken als ze
smelten. En die waarde heeft een behoorlijk gedetermineerde (gemiddelde) waarde
met enige maar niet zeer grote spreiding. Maar die eigenlijk pas gaat tellen
indien van toepassing in grote hoeveelheden. In welke hoeveelheden geen enkele
sneeuwvlok ooit als individu zal worden gezien. Je
begint een overgangsgebied te raken zodra moleculen in vaste vorm komen. Hier
rechts staat een illustratie van sneeuwvlokken - overduidelijk allemaal met een
hoogst individuele structuur, en hier is op zicht al van toepassing: "Er is er
geen een hetzelfde".
Desalniettemin is het volkomen ongebruikelijk om sneeuwvlokken als individuen te
zien. Van individuele sneeuwvlokken telt voor zover het mensen betreft slechts
één enkele waarde: de hoeveelheid warmte die ze aan de omgeving onttrekken als ze
smelten. En die waarde heeft een behoorlijk gedetermineerde (gemiddelde) waarde
met enige maar niet zeer grote spreiding. Maar die eigenlijk pas gaat tellen
indien van toepassing in grote hoeveelheden. In welke hoeveelheden geen enkele
sneeuwvlok ooit als individu zal worden gezien.
De mate van individueel-zijn versus groepslid-zijn hangt dus mede af van hoe
gedetailleerd je naar de situatie kijkt. Bij sneeuwvlokken is dat dus
(normaliter) zeer weinig. Stappende op de ladder van de levende natuur en gaande
omhoog wordt dat dus progressief meer. Tot aan komende bij de mens, waar er hele
volksstammen en bijna complete wetenschappelijke disciplines zijn die beweren
dat het ongeldig is te spreken over een mens als groepslid - volgens die
opvatting zijn mensen uitsluitend individuen.
Bovenstaand is al impliciet afstand genomen van deze ideeën middels de
anti-antropocentrische stellingname dat datgene wat voor de natuurkundige generalisaties
geldt, ook geldt voor alle andere generalisaties tenzij anderzijds blijkt.
En dit was ook het uitgangspunt van Asimov in Foundation zoals genoemd in
de inleiding van Psycho-socio-historie
 : neem genoeg mensen, en het gedrag van de groepen is even gedetermineerd als
dat van sneeuwvlokken. Dat wil zeggen: in beide gevallen met uitzonderingen
bepaald door het uit de hand lopen van bepaalde parameters, op het niveau van
sneeuw door zoiets als "smelten", en op het niveau van mensen door iets dat
lijkt op "revolutie". Waarvoor in het geval dan Asimov dan noodzakelijke
hoeveelheden ter hoogte van duizenden planeten wordt verondersteld.
: neem genoeg mensen, en het gedrag van de groepen is even gedetermineerd als
dat van sneeuwvlokken. Dat wil zeggen: in beide gevallen met uitzonderingen
bepaald door het uit de hand lopen van bepaalde parameters, op het niveau van
sneeuw door zoiets als "smelten", en op het niveau van mensen door iets dat
lijkt op "revolutie". Waarvoor in het geval dan Asimov dan noodzakelijke
hoeveelheden ter hoogte van duizenden planeten wordt verondersteld.
Met de introductie van de term "revolutie" is al duidelijk dat ook voor de
huidige hoeveelheden mensheid veel zaken besproken en geanalyseerd kunnen worden
in de termen van groepen en groepsgedrag. Het veroordelen van groepsgedrag is
daarvan eigenlijk een aanvullende ondersteuning, want de stelling dat de
mensheid niet kan worden beschreven in groepsgedrag, is zo absurd
(niveau: "De maan is van groene kaas") dat ze alleen door groepsgedrag zichzelf
kan verspreiden. Dit geheel analoog waarop de monotheïstische religie is en
wordt verspreid, en andere vormen van ideologie, ooit door bioloog Richard
Dawkins
 omschreven als "memen"
omschreven als "memen"
 .
.
Voor de huidige omvang van de mensengroepen is het wel zo dat de vaagheid van de
begrenzing ervan een aanzienlijke invloed heeft op de processen die ze
ondergaan. Met die vaagheid moet dus rekening gehouden worden in de beschrijving
en de modellen. De beschrijving van die vaagheid is natuurlijk weer het
makkelijkst voor een extreem geval: een verzameling elementen slechts één
specifieke eigenschap die volkomen willekeurig verdeeld is. Een probleem dat
onder historische wiskundigen bekend raakte door een mondaine bezigheid: het
kaartspel. Wat nog verder gereduceerd kan worden tot het gooien van
dobbelstenen. Waarvan voor grote aantallen stenen de uitkomst bekend is: dat
levert de normale of Gauss-verdeling op. Wat precies dezelfde verdeling is als
die van het Galton board, als je genoeg knikkers en gaatjes neemt. Voor
de bespreking van de normale verdeling, zie hier
 .
.
Naar Evolutie
 , of
site home
, of
site home
 ·. ·.
|