De algemene groeiwetten
Als er een wedstrijd gehouden zou worden omtrent wat de belangrijkste natuurwet
is, zou de groeiwet een goede kans maken. De groeiwet maakt het mogelijk
dat levende organismen van enige omvang zich kunnen ontwikkelen. Alle levende
organismen beginnen namelijk met een enkele cel, bij mensen de bevruchte eicel,
die een minuscule omvang en gewicht heeft. Om daaruit een mens van twee meter en
tientallen kilos te maken, moet er razendsnel gegroeid worden. Dat gaat volgens
de methodiek: 1, 2, 4, 8, 16, 32, 64, enzovoort - iedere keer deelt ieder
celletje zich in tweeën, het totaal aantal verdubbelend.
Merk als eerste eigenschap op dat niet alleen het getal zelf groter
wordt, maar ook de stap naar de volgende - die toename heeft dezelfde vorm, maar
loopt als het ware een stapje achter: 1, 2, 4, 8, 16, 32, enzovoort.
Hoe snel dit gaat is bekend uit het verhaal van de uitvinder van het
schaken die zich door de koning liet uitbetalen met het aantal rijstkorrels dat
je op die manier van een schaakbord, met 64 velden, zou kunnen halen. De
betrokken hoeveelheid is astronomisch
 (Wikipedia).
(Wikipedia).
Deze vorm van groei heet exponentiële groei - het is van alle simpelere manieren
om groei wiskundig voor te stellen de sterkste vorm van groei - bijvoorbeeld die
van de kwadraten: 1, 4, 9, 16, 25, 36, 49, enzovoort lijkt ook snel te gaan,
maar de exponentiële groeit gaat altijd sneller.
De
exponentiële groei wordt meestal uitgedrukt in een functie vergezeld van een
grafiek, zie onder:
De "x" in de rode versie staat voor het aantal malen
dat je met 2 vermenigvuldigt. Natuurlijk kan je ook andere getallen gebruiken
zoals de eveneens afgebeelde 3 (1, 3, 9, 27, 81, enzovoort) en 4, die natuurlijk
nog steiler gaan.
Het tweede belangrijke praktische voorbeeld van de exponentiële functie is die
van de samengestelde interest op spaartegoeden. Als je een bedrag op een bank
stoort en daarbij 5 procent rente krijgt, en die rente niet opneemt maar op de
rekening laat storten, krijg je ook een exponentiële reeks. Na tien jaar sparen,
is er niet 10 maal 5 procent is 50 procent erbij, maar (1,05) x (1,05) x ....
enzovoort (of: (1,05)10 ) , en dat is 63
procent - en na 20 jaar is heb je niet het dubbele, maar 2,6 keer zoveel. Deze
functie schijf je als y = 1,05x waarbij x het
aantal jaren is en y het bedrag op de rekening, als je met 1 euro begon.
Dat de groeiwet zo veel voorkomt, is makkelijk te begrijpen, als je
veralgemeniseerd wat er over de eerste, de verdubbelaar, werd gezegd: de toename
neemt ook toe, en wel evenredig met hoe groot je op dat moment al bent: ben je 4
komt er 4 bij, ben je 16, komt er 16 bij.
Dat dit zelfs al bij kleine percentages een belangrijke factor is, blijkt uit
het voorgaande praktijkvoorbeeld (de Volkskrant, 24-11-2012, van
verslaggeefster Yvonne Hofs):
De grafiek toont op dramatische wijze de invloed van kosten ten grootte van
slechts 2 procent per jaar: de opbrengst na 20 jaar daalt met ongeveer de helft.
Dat de groei afhangt van wat je al hebt, is voor iets als rente zelfs
vanzelfsprekend. En daarom is de groeiwet zo veel voorkomend: hij slaat op
celletjes komende uit een eicel, bacteriën op een kweekschaaltje, bacteriën in
de mens, eendekroos op de sloot, en mensjes komende uit mensjes:
Andere toepassingen zijn te vinden in de psychologie bij valkuilen
 ,
in de sociologie bij bevolkingsgroei ,
in de sociologie bij bevolkingsgroei
 ,
in de economie bij de vrije markt ,
in de economie bij de vrije markt
 ,
en in de financiële wereld bij kuddegedrag ,
en in de financiële wereld bij kuddegedrag
 .
.
Uit de wiskundige eigenschappen van de groeiwet zijn een aantal in woorden
geformuleerde regels af te leiden. De eerste is logisch:
Groeiwet 1: Bij gelijke groeifactor, wint de grootste het altijd van de
kleinere, en het verschil wordt steeds sneller steeds groter.
Dus als je begint met twee mensen, en de een heeft, zeg,1000 euro en de ander
2000 euro, en hun kapitaal verdubbelt ieder jaar, dan is het verschil na 5 jaar
32 duizend euro. Voor kleinere groeifactoren duurt het langer, maar uiteindelijk
gebeurt hetzelfde.
De tweede groeiwet is wat minder voor de hand liggend:
Groeiwet 2: De grotere groeifactor wint het altijd van de kleinere, en dat is
onafhankelijke van de twee aanvangsgroottes.
Dit is makkelijker in te zien door het in twee stappen te verdelen. Stel het ene
kapitaal is 200 euro en het tweede is 1000 euro, maar de eerste verdubbelt en de
tweede gaat iedere keer maar met 1,5 omhoog. De eerste gaat 200, 400, 800,1600,
3200, 6400, 12800, enzovoort, en de tweede 1000, 1500, 2250, 3375, 5062,5,
7593,75 , 11390,625 - en vanaf dit punt geldt al hetzelfde als in groeiwet 1,
want de kleinere is nu al de grotere geworden.
Deze twee basale groeiwetten hebben evenveel toepassingen als het exponentiële
groeiproces zelf. Een belangrijke economische toepassing is deze: Als de twee
partijen ergens in concurrentie raken waarbij het er ook om gaat wie het hoogste
bedrag kan bieden, prijst de grotere de kleinere uiteindelijk altijd uit de
markt.
Dit voorlopig wat betreft de vrije exponentiële groei. Nu terug naar de vraag
wanneer de exponentiële groei niet geldt: Ook dat is bekend: als de
ruimte of grondstoffen opraken. Op een gegeven moment is de voedingsstof voor de
bacteriën in het kweekschaaltje op, gaat de door een virus ziek gemaakte mens
dood, raakt het slootje vol kroos, en is de aarde uitgeput.
 Meestal
is dat uitgeput raken van de voorraden al merkbaar voordat het einde van de
groei is gekomen. Je ziet voordien al dat de groei steeds minder snel gaat, en
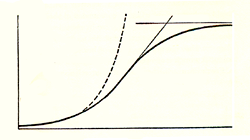
pas geleidelijk staat de groei helemaal stil. Dit ziet er in zijn archetypische
vorm uit als hiernaast. De stippellijn is het vervolg van de exponentiële groei
zonder remming. In het midden van de grafiek zie je dat de groei een korte tijd
constant is - daar is de groeisnelheid tevens maximaal. En uiteindelijk nadert
het aantal of de grootte steeds dichter naar een constante waarde. Meestal
is dat uitgeput raken van de voorraden al merkbaar voordat het einde van de
groei is gekomen. Je ziet voordien al dat de groei steeds minder snel gaat, en
pas geleidelijk staat de groei helemaal stil. Dit ziet er in zijn archetypische
vorm uit als hiernaast. De stippellijn is het vervolg van de exponentiële groei
zonder remming. In het midden van de grafiek zie je dat de groei een korte tijd
constant is - daar is de groeisnelheid tevens maximaal. En uiteindelijk nadert
het aantal of de grootte steeds dichter naar een constante waarde.
Ook dit proces is uiterst veelvoorkomend. Planten, dieren, mensen: allemaal
begint klein, groeit steeds sneller, tot ergens in het midden, en groeit steeds
langzamer tot de maximale hoogte. Niet zo mooi als in de grafiek, maar wel iets
dat er op lijkt. Zelfs allerlei niet-natuurlijk lijkende processen zoals de
ontdekking van de chemische elementen of grondstoffenproductie hebben een
soortgelijke vorm, zoals beschreven door Derek de Solla Price
 in Little science, big science.
in Little science, big science.
Deze vorm van het tot stilstand komen van exponentiële groei is de
"gewenste" - er gebeurt niets dramatisch met eventuele contraproductieve
gevolgen. Maar dit kan ook anders aflopen.
 Het
eerste geval van contraproductieve afloop doet zich voor als er wel een remmende
factor is, maar geen geleidelijkheid in de toename ervan - hij treed in één keer
op. Het archetypische voorbeeld is dat van een ongeremde bacteriële of virale
infectie in een menselijk of dierlijk lichaam: de bacterie groeit ongeremd, tot
het gastlichaam doodgaat - kort daarna gaat de bacterie ook dood. Het
groeiproces eindigt abrupt. Het
eerste geval van contraproductieve afloop doet zich voor als er wel een remmende
factor is, maar geen geleidelijkheid in de toename ervan - hij treed in één keer
op. Het archetypische voorbeeld is dat van een ongeremde bacteriële of virale
infectie in een menselijk of dierlijk lichaam: de bacterie groeit ongeremd, tot
het gastlichaam doodgaat - kort daarna gaat de bacterie ook dood. Het
groeiproces eindigt abrupt.
De natuur "leert" dat ook, en de oudere bacteriën en virussen
maken het gastlichaam niet dood, maar ziek - bij voorkeur gepaard gaand met een
mechanisme voor verdere verspreiding, zoals het verkoudheidvirus dat doet
middels een snotterende neus.
 Het
tweede geval is dat waarbij groeifactor en remfactor een invloed op elkaar
uitoefenen. Dat leidt tot een diversiteit aan gevolgen. Een bekend voorbeeld
daarvan is het verhaal van de vossen en konijnen. Stel je hebt een ruim
duingebied bewoond door grote populatie konijnen. Nu laat je er een stelletje
vossen los. Die vossen hebben dan ruim te eten, en dus krijgen ze veel jongen -
je ziet een een periode van exponentiële groei. Dus komen er veel vossen, en
gaat het aantal konijnen steeds sterker achteruit - en vlakt de groei van het
aantal vossen af. Als de konijnen dan uiteindelijk aan het opraken zijn, sterven
de vossen van de honger, en gaat hun aantal achteruit. Als het aantal vossen
aanzienlijk gedaald is, herstelt de konijnenpopulatie zich. Dus komen er weer
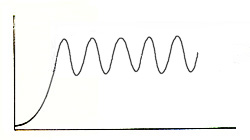
meer vossen - enzovoort. In de grafiek ziet je het aantal vossen toe- en afnemen
in een oscillerend patroon. Het
tweede geval is dat waarbij groeifactor en remfactor een invloed op elkaar
uitoefenen. Dat leidt tot een diversiteit aan gevolgen. Een bekend voorbeeld
daarvan is het verhaal van de vossen en konijnen. Stel je hebt een ruim
duingebied bewoond door grote populatie konijnen. Nu laat je er een stelletje
vossen los. Die vossen hebben dan ruim te eten, en dus krijgen ze veel jongen -
je ziet een een periode van exponentiële groei. Dus komen er veel vossen, en
gaat het aantal konijnen steeds sterker achteruit - en vlakt de groei van het
aantal vossen af. Als de konijnen dan uiteindelijk aan het opraken zijn, sterven
de vossen van de honger, en gaat hun aantal achteruit. Als het aantal vossen
aanzienlijk gedaald is, herstelt de konijnenpopulatie zich. Dus komen er weer
meer vossen - enzovoort. In de grafiek ziet je het aantal vossen toe- en afnemen
in een oscillerend patroon.
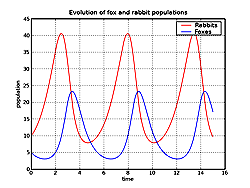 Deze
soort gedrag leent zich prima voor wiskundige modellering - dat van de vossen en
konijnen heet: twee gekoppelde vergelijkingen. Nevenstaande grafiek is gemaakt
met een computer die de vergelijkingen heeft uitgerekend, met in het rood het
aantal konijnen, en in het blauw het aantal vossen. Deze
soort gedrag leent zich prima voor wiskundige modellering - dat van de vossen en
konijnen heet: twee gekoppelde vergelijkingen. Nevenstaande grafiek is gemaakt
met een computer die de vergelijkingen heeft uitgerekend, met in het rood het
aantal konijnen, en in het blauw het aantal vossen.
Het geval van vossen en konijnen verschilt van dat van de bacteriën in het
kweekschaaltje dat in het tweede geval het opraken van de voedingsbron een
constante factor is, terwijl in het eerste geval de konijnen, de voedingsbron
van de vossen, een eigen dynamiek hebben - het als het ware of het
"kweekschaaltje" van de vossen voortduren krimpt en uitdijt. Omdat de groei van
het aantal konijnen ook een exponentieel proces is, heb je hier dus te maken met
twee exponentiële processen: de groei van zowel vossen als konijnen. Het
algemene geval van de combinatie van twee exponentiële processen die elkaar
beïnvloeden leidt, ook wiskundig, tot oscillaties als in de grafiek - in het
speciale geval dat de twee groeifactoren even groot zijn, krijg je mooie ronde
sinussen, de vorm die ook meestal gebruikt wordt om oscillaties weer te geven.
Het geval van de vossen en konijnen staat voor talloze andere praktische
situaties. Het is ook bekend als de varkenscyclus: als varkensvlees duur is,
krijgen veel boeren het idee om een varkensstal in te richten, er komt meer
varkensvlees op de markt, de prijs daalt, enzovoort. Ook de bestuurlijke variant
is goed bekend: er zijn te veel tandartsen, de regering sluit een aantal
klinieken, enzovoort ... - in al dit soort gevallen draait het om overreactie.
 Naast
de twee groeifactoren is er meestal nog een derde soort factor in het spel: de
demping. Dat is het makkelijkst uit te leggen aan de hand van een mechanisch
geval: als je een gewicht aan een veertje hangt, het gewicht-met-veertje uitrekt
en dan het gewicht loslaat, gaat het op dezelfde manier oscilleren als het
aantal vossen en konijnen. Maar de beweging veroorzaakt wrijving, en daardoor
komt het geheel uiteindelijk in de evenwichtsstand tot stilstand - je ziet het
patroon van de grafiek rechtsboven. Naast
de twee groeifactoren is er meestal nog een derde soort factor in het spel: de
demping. Dat is het makkelijkst uit te leggen aan de hand van een mechanisch
geval: als je een gewicht aan een veertje hangt, het gewicht-met-veertje uitrekt
en dan het gewicht loslaat, gaat het op dezelfde manier oscilleren als het
aantal vossen en konijnen. Maar de beweging veroorzaakt wrijving, en daardoor
komt het geheel uiteindelijk in de evenwichtsstand tot stilstand - je ziet het
patroon van de grafiek rechtsboven.
De uiteindelijke uitkomst van dit soort processen is dus toch meestal weer een
vorm van evenwicht: als de populatie in één keer uitsterft, is dat ook
evenwicht, zij het een heel saai. Alleen mensen willen nog wel eens hardnekkig
zijn, en doorgaan met hun ongecontroleerde bijstuurgedrag - in de natuur zijn
evenwichtssituaties de meest voorkomende. Wat er zoal gebeurt in de wereld is dus
meestal de verstoring van bestaande evenwichtssituaties. Daarover meer hier
 . .
Naar Evolutie
 , of site home
, of site home
 ·. ·.
|