Evenwichtsverschijnselen
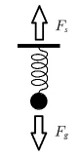 Onder evenwichtssituaties verstaan natuurkundigen die situaties die tot stand
zijn gekomen onder de invloed van twee of meer elkaar tegenwerkende krachten,
die in de evenwichtssituatie "toevalligerwijs" precies even groot zijn. Het
bekende middelbare school-voorbeeld is dat van een gewichtje dat aan een touwtje of
elastiekje hangt: de zwaartekracht trekt aan het gewichtje naar beneden, en het
elastiekje trekt aan het gewichtje naar boven - en als het gewichtje stil hangt,
zijn die krachten "in evenwicht" - dan hebben we een "evenwichtssituatie". Onder evenwichtssituaties verstaan natuurkundigen die situaties die tot stand
zijn gekomen onder de invloed van twee of meer elkaar tegenwerkende krachten,
die in de evenwichtssituatie "toevalligerwijs" precies even groot zijn. Het
bekende middelbare school-voorbeeld is dat van een gewichtje dat aan een touwtje of
elastiekje hangt: de zwaartekracht trekt aan het gewichtje naar beneden, en het
elastiekje trekt aan het gewichtje naar boven - en als het gewichtje stil hangt,
zijn die krachten "in evenwicht" - dan hebben we een "evenwichtssituatie".
In Evolutie
 hebben we het natuurlijke ontstaan van evenwicht verbonden met het begrip
terugkoppeling, nader beschreven hier
hebben we het natuurlijke ontstaan van evenwicht verbonden met het begrip
terugkoppeling, nader beschreven hier
 . Ook de situatie van gewicht-en-veertje kan gezien worden als een vorm van terugkoppeling. Want als
je het gewichtje eerst in de hand houdt en langzaam laat zakken, wordt de veer
steeds verder uitgerekt waardoor de tegenwerkende kracht steeds groter wordt. Net
zo lang dat hij even sterk als de zwaartekracht. En ga je te ver door,
dan zorgt de extra kracht van de veer dat het gewichtje toch weer terug gaat naar het
evenwicht. Ga je uit van de evenwichtssituatie, dan is het zo dat de kracht van
de veer steeds wordt "aangepast" aan de afwijking vanuit het evenwicht terug
naar dat evenwicht. Dat wil zeggen: dat evenwicht is blijvend door een
automatisch proces van terugkoppeling.
. Ook de situatie van gewicht-en-veertje kan gezien worden als een vorm van terugkoppeling. Want als
je het gewichtje eerst in de hand houdt en langzaam laat zakken, wordt de veer
steeds verder uitgerekt waardoor de tegenwerkende kracht steeds groter wordt. Net
zo lang dat hij even sterk als de zwaartekracht. En ga je te ver door,
dan zorgt de extra kracht van de veer dat het gewichtje toch weer terug gaat naar het
evenwicht. Ga je uit van de evenwichtssituatie, dan is het zo dat de kracht van
de veer steeds wordt "aangepast" aan de afwijking vanuit het evenwicht terug
naar dat evenwicht. Dat wil zeggen: dat evenwicht is blijvend door een
automatisch proces van terugkoppeling.
De meeste situaties in de natuur zijn evenwichtssituaties. De reden
daarvan is meteen duidelijk als je het elastiekje doorbrandt. Zodra je het zo
ver hebt doorgebrand dat de zwaartekracht wint, dat wil zeggen: dat het
elastiekje breekt, valt het gewicht naar beneden en heb je een
niet-evenwichtssituatie. Maar die duurt maar heel even. Het gewichtje valt met
een klap op de grond, waarna de grond de rol van het elastiekje overneemt - want
de grond houdt, net als het elastiekje, het gewichtje tegen. Niet door uit te
rekken, maar door een beetje ingedrukt te worden - doe het experiment met een
groot gewicht en zachte grond, dan kan je dat zo zien. De regel is dus:
niet-evenwichtssituaties duren kort, en zijn tussentoestanden tussen
evenwichtssituaties.
Die evenwichtssituaties hoeven niet per se altijd hetzelfde te
blijven, maar kunnen ook langzaam veranderen - dat noemen natuurkundigen
"quasi-stationaire" veranderingen. Het langzame rekken van het elastiekje
terwijl je het aan het doorbranden bent, is zo'n quasi-stationaire verandering.
Je kan dit het geval van "langzaam meegeven" noemen.
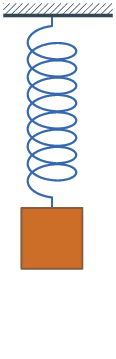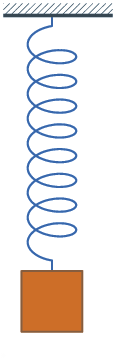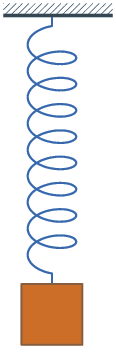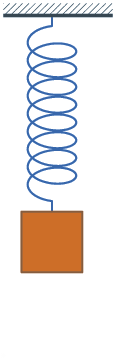  Er
gebeuren andere dingen als je een evenwichtssituatie blootstelt aan een snelle
verandering, in het geval van elastiek-en-gewicht door er een stoot tegen te
geven. Het is algemeen bekend wat er dan gebeurt: het gewicht gaat om de
evenwichtstand heen en weer wiebelen - netjes gezegd: "oscilleren", zie de
illustratie links. Als je de hoogte van het gewicht (boven de grond) uitzet in
een grafiek, krijg je de illustratie rechtsboven. Er
gebeuren andere dingen als je een evenwichtssituatie blootstelt aan een snelle
verandering, in het geval van elastiek-en-gewicht door er een stoot tegen te
geven. Het is algemeen bekend wat er dan gebeurt: het gewicht gaat om de
evenwichtstand heen en weer wiebelen - netjes gezegd: "oscilleren", zie de
illustratie links. Als je de hoogte van het gewicht (boven de grond) uitzet in
een grafiek, krijg je de illustratie rechtsboven.
 De
animatie van de oscillerende veer is handig voor een demonstratie, maar niet
representatief voor de werkelijkheid. In de werkelijkheid duurt het oscilleren
slechts korte(re) tijd, en komt het geheel tot stilstand vanwege de wrijving,
zie de illustratie rechtsboven . Het algemene geval van het afnemen van de
heftigheid van de oscillaties heet "demping". De
animatie van de oscillerende veer is handig voor een demonstratie, maar niet
representatief voor de werkelijkheid. In de werkelijkheid duurt het oscilleren
slechts korte(re) tijd, en komt het geheel tot stilstand vanwege de wrijving,
zie de illustratie rechtsboven . Het algemene geval van het afnemen van de
heftigheid van de oscillaties heet "demping".
Dit zijn de belangrijkste eigenschappen van een simpele
evenwichtssituatie als die van een gewicht en een elastiek of veer. Een
dergelijk evenwicht kan in de praktijk alleen tot stand komen als minstens één
van de betrokken krachten veranderlijk is - heb je twee verschillende constante
krachten, is er geen enkele reden dat ze even groot zouden zijn. Die verandering
moet dan ook nog zo zijn dat bij een afwijking van het evenwicht de kracht
terugstuurt naar het evenwicht, en liefst ook nog groter naarmate de toestand
verder van het evenwicht raakt. In het schoolvoorbeeld is de veranderlijke
kracht natuurlijk die in het elastiek: hoe verder je het rekt, hoe meer het
terugtrekt.
In de praktijk blijken toch vele processen op die manier te werken.
Deels ook weer om de eenvoudige reden dat processen die niet zo werken, niet
veel kans hebben om tot een evenwicht te komen. In de materiële wereld zijn
bekende krachten die de gewenste eigenschappen hebben de zwaartekracht en de
elektrische kracht. Van de zwaartekracht leidt dat tot stabiele systemen als
"zon met planeten"-stelsels afgekort tot zonnestelsels, voor de elektrische kracht tot atomen, moleculen,
enzovoort.
Waar het hier op deze website om gaat, zijn processen in de
menselijke wereld en de menswetenschappen. Ook dan gaat het om processen rond
toestanden die grotendeels gezien kunnen worden als evenwichtsprocessen
 . Ook in de menswetenschappen zijn niet-evenwichtsprocessen een zeldzaamheid,
die men kent in de sociologie als "opstand" en "revolutie", en in de psychologie
als "neurose" en "psychose".
. Ook in de menswetenschappen zijn niet-evenwichtsprocessen een zeldzaamheid,
die men kent in de sociologie als "opstand" en "revolutie", en in de psychologie
als "neurose" en "psychose".
Evenwichtsprocessen in de menselijke wereld komen vaak op een
ingewikkeldere manier tot stand, omdat er meestal meer dan twee krachten of
invloeden zijn bij betrokken. Ingewikkeldere processen komen moeilijker tot een
evenwichtstand, en door mensenhanden gemaakte ingewikkelde processen hebben
daarom vaak een speciaal deelproces dat er specifiek voor bedoeld is om het
evenwicht te maken en/of te handhaven. Dat speciale proces werkt vrijwel altijd
met terugkoppeling: de huidige toestand wordt vergeleken met een gewenste, en
bij een afwijking wordt het systeem bijgestuurd zodat het weer teruggaat naar de
evenwichtsstand. De door de natuur gemaakte ingewikkelde processen, met name de
biologische, hebben vaak ook een apart deelproces middels terugkoppeling dat
voor het evenwicht zorgt - een voorbeeld is de biologisch klok, die standaard
afgesteld staat op een ritme van 25 uur, en door het dag-nachtverschijnsel
ingeregeld wordt tot 24 uur - het is dit systeem dat van slag raakt en opnieuw
bijgesteld wordt onder de naam "jetlag". Meer over het verschijnsel van
terugkoppeling hier
 .
.
Dit alles is van essentieel belang zodra je de wens krijgt om iets
aan een toestand iets te veranderen. Je mag er vanuit gaan dat het een
evenwichttoestand betreft, en dat het bovenstaande van toepassing is. Voor een
simpel(er) systeem wil dat zeggen: als je denkt om met een flinke stoot de
huidige
evenwichtstand te veranderen, kom je bedrogen uit: de toestand gaat rond die
bestaande evenwichtstand slingeren, en komt daar weer na kortere of langere tijd
weer op uit. Ook veel ingewikkelder lijkende systemen vertonen dit soort gedrag.
Maar bij een ingewikkeld(er) systeem kan het ook anders liggen anders. Een
aantal ingewikkelder
systeem heeft meerdere evenwichtstoestanden. Er zijn dan twee
manieren om het systeem van evenwichtstand te veranderen: een kleine maar
langdurig werkende kracht die het systeem langzaam naar de nieuwe evenwichtstand
brengt, of een krachtige korte stoot in de juiste richting. Beide methodes
hebben hun voor- en nadelen.
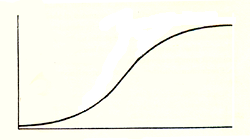 Het voordeel van de methode van de kleine maar gestage kracht is
dat je zeker weet dat je in de goede richting gaat. Idealiter ziet het er dan
uit zoals rechts: de horizontale as is de oude waarde, en het systeem beweegt
zich geleidelijk naar de nieuwe waarde. Met als voordeel dat het in één keer
naar de gewenste waarde gaat. Maar met als nadeel dat het het lang kan duren - wat ook te lang kan zijn. Een andere mogelijk nadeel is het feit dat
het soms niet kan: soms wordt een kleine kracht gecompenseerd door een andere
tegenkracht in het systeem, bijvoorbeeld "wrijving" van diverse soorten, die de kleine kracht compenseert - het systeem
blijft in dezelfde evenwichtstand hangen. Dit heeft soort verschijnsel heeft de
algemene naam van een "kritieke waarde", een waarde waar je boven moet zitten om
iets te bereiken. Het voordeel van de methode van de kleine maar gestage kracht is
dat je zeker weet dat je in de goede richting gaat. Idealiter ziet het er dan
uit zoals rechts: de horizontale as is de oude waarde, en het systeem beweegt
zich geleidelijk naar de nieuwe waarde. Met als voordeel dat het in één keer
naar de gewenste waarde gaat. Maar met als nadeel dat het het lang kan duren - wat ook te lang kan zijn. Een andere mogelijk nadeel is het feit dat
het soms niet kan: soms wordt een kleine kracht gecompenseerd door een andere
tegenkracht in het systeem, bijvoorbeeld "wrijving" van diverse soorten, die de kleine kracht compenseert - het systeem
blijft in dezelfde evenwichtstand hangen. Dit heeft soort verschijnsel heeft de
algemene naam van een "kritieke waarde", een waarde waar je boven moet zitten om
iets te bereiken.
Een verschijnsel lijkend op dat van de kritieke waarde is dat van
het "kantelpunt" of "tipping point": je moet het systeem voorbij een
bepaalde stand duwen, waarna het vaak vanzelf doorloopt naar de nieuwe
evenwichtstand. Dit is een analogie van de situatie dat je een bal tegen een
heuveltje op naar boven schiet (bijvoorbeeld bij het golfen): de bal moet
voorbij het bovenste punt van de heuvel raken, anders rolt hij weer terug.
 Nauw
verwant aan het "kantelpunt" is het verschijnsel van "overschieten": eenmaal
voorbij het kantelpunt, als de toestand vanzelf naar de nieuwe evenwichtswaarde
beweegt, gebeurt het ook dat door de snelheid waarmee de evenwichtswaarde
bereikt, het systeem doorschiet voorbij de evenwichtswaarde. Als het systeem
daarna toch weer teruggaat naar de evenwichtswaarde, krijg je het patroon van de
illustratie rechtsboven. Dit kan een bezwaar zijn, als de toestand van het
systeem niet boven een bepaalde waarde mag komen. Dan is extra demping gewenst.
Voorbeelden uit de menswetenschappen zijn gegeven hier Nauw
verwant aan het "kantelpunt" is het verschijnsel van "overschieten": eenmaal
voorbij het kantelpunt, als de toestand vanzelf naar de nieuwe evenwichtswaarde
beweegt, gebeurt het ook dat door de snelheid waarmee de evenwichtswaarde
bereikt, het systeem doorschiet voorbij de evenwichtswaarde. Als het systeem
daarna toch weer teruggaat naar de evenwichtswaarde, krijg je het patroon van de
illustratie rechtsboven. Dit kan een bezwaar zijn, als de toestand van het
systeem niet boven een bepaalde waarde mag komen. Dan is extra demping gewenst.
Voorbeelden uit de menswetenschappen zijn gegeven hier
 .
.
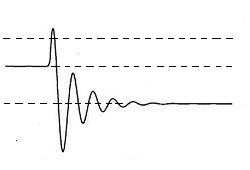 Na
het uitoefenen van een gestage kracht is het doorschieten meestal geen probleem.
Dat is anders als je in plaats van een gestage kracht, en snelle en krachtige
stoot tegen het systeem geeft. Het systeem gaat dan sterk oscilleren, en kan dan
vaak meerdere nieuwe evenwichtsstanden bereiken, waaronder ook die aan de andere
kant liggen van wat men wenst, zie de figuur hiernaast (waarin de bedoeling was
om een nieuwe evenwichtstand naar boven te bereiken). In het algemeen is daarbij
een van de regels dat welk evenwicht het wordt, onderhevig is aan
waarschijnlijkheden en niet aan zekerheden. Een bekend voorbeeld van dit
verschijnsel is dat het resultaat van een revolutie tegen een dictatuur, wel
eens een nog ergere dictatuur kan zijn. Na
het uitoefenen van een gestage kracht is het doorschieten meestal geen probleem.
Dat is anders als je in plaats van een gestage kracht, en snelle en krachtige
stoot tegen het systeem geeft. Het systeem gaat dan sterk oscilleren, en kan dan
vaak meerdere nieuwe evenwichtsstanden bereiken, waaronder ook die aan de andere
kant liggen van wat men wenst, zie de figuur hiernaast (waarin de bedoeling was
om een nieuwe evenwichtstand naar boven te bereiken). In het algemeen is daarbij
een van de regels dat welk evenwicht het wordt, onderhevig is aan
waarschijnlijkheden en niet aan zekerheden. Een bekend voorbeeld van dit
verschijnsel is dat het resultaat van een revolutie tegen een dictatuur, wel
eens een nog ergere dictatuur kan zijn.
Als je dus de evenwichtstoestand van een ingewikkeld systeem wilt
veranderen, en meer zekerheid wilt hebben over het nieuwe evenwicht, dan is de
stoot, een plotselinge korte sterke kracht, of ook wel de "shocktherapie", niet
het geëigende gereedschap. Dan is het beter te kiezen voor het model van de
kleinere maar langdurige kracht, oftewel de geleidelijke aanpak. In de taal van
het evenwichtsproces: de quasi-stationaire verandering. In sociologische termen:
evolutie boven revolutie. In welke laatste vorm het gezien wordt als een bijna
vanzelfsprekendheid.
Maar dat geldt lang niet overal in de maatschappij. Vooral het bedrijfsleven zit vol met neigingen tot
de niet geleidelijke aanpak: de uitvoering van de wens tot omzetvergroting door
bedrijfsovername, de oplossing van financiële problemen door reorganisatie en
massaontslag, en dergelijke, zijn vormen van shocktherapie die lijken op
de stoot-methode van verandering.
Rijst wel de vraag hoe men kan bepalen wat in diverse
omstandigheden gezien kan worden als een snelle en een langzame verandering. Als
men het systeem enigszins redelijk kan modelleren, is de oplossing simpel: dan
zegt de wiskunde wat langzaam en snel is. Kan dat niet, is het mogelijk te
kijken naar de reacties op voorgaande veranderingen, daarbij ook soortgelijke
systemen meenemende. Voor de simpelere gevallen kan men het zelfs wel met enige
intuïtie af: hoe zwaarder het gewicht aan het elastiek, hoe langzamer je de
kracht moet opvoeren.
Een "gewone" veer-met-gewicht uit het schoolexperiment trilt typisch in de buurt
van seconden, dus een "stoot" is dan iets van een tiende seconden.
Maatschappijen veranderen over de generaties, dus een "stoot" kan dan jaren of
enkele tientallen jaren lang duren. Zoals de naoorlogse immigratiegolf in
Nederland (in de buurt van 10 procent van de bevolking in circa 20 jaar erbij)
duidelijk als een stoot heeft gewerkt - de effecten "golven" nog steeds na.
Het voorgaande ging over de beïnvloeding van een evenwicht van
buiten - in psychologische termen: een prikkel. Het andere geval is verandering
van het evenwicht ten gevolge van processen van binnen - hetgeen natuurlijk dan
vrijwel altijd ingewikkeldere systemen betreft. Van buiten zie je dit als een
spontane verandering - van binnen liggen er meestal concrete zaken aan ten
grondslag - een emotionele uitbarsting lijkt voor een vreemde een spontaan
gebeuren, maar voor de therapeut van de betrokkene is het een gevolg van een
jeugdtrauma - bijvoorbeeld. Het sociologische archetype is natuurlijk weer dat
van een revolutie: voor betrokkenen meestal onverwacht, voor de historici
meestal goed te verklaren
 . .
Een veelvoorkomend geval van interne prikkeling of verandering, ook
wel een "autonoom" proces genoemd, is groei. Dit proces is uitgewerkt in
Groeiwetten
 , met als archetypische voorbeelden dat van de begroeiing van een sloot door
eendekroos of de groei van zoiets als een bonenstaak, het begint langzaam en
gaat steeds sneller. Tenzij er iets anders komt dat een tegenwicht biedt, zorgt
voor evenwicht, kan de zaak uit de hand lopen. Als er sprake is van een eveneens
groeiend tegenwicht, krijt je de de S-vormige curve van de geleidelijke
verandering, hierboven.
, met als archetypische voorbeelden dat van de begroeiing van een sloot door
eendekroos of de groei van zoiets als een bonenstaak, het begint langzaam en
gaat steeds sneller. Tenzij er iets anders komt dat een tegenwicht biedt, zorgt
voor evenwicht, kan de zaak uit de hand lopen. Als er sprake is van een eveneens
groeiend tegenwicht, krijt je de de S-vormige curve van de geleidelijke
verandering, hierboven.
Een voorbeeld van zo'n tegenwicht is het (archetypische) geval van de vossen en konijnen: beide groeien exponentieel bij
voldoende voedingsmateriaal: voor konijnen: gras, en voor vossen: konijnen. Op
een gegeven moment kunnen vossen, konijnen en gras elkaar dus mooi in evenwicht
houden: de konijnen eten het gras, maar als er te veel komen en het gras op zou
kunnen raken, stijgt ook het aantal vossen, zodat het aantal konijnen weer
afneemt. Enzovoort.
De natuur zit zodanig vol met dit soort evenwichten dat daar op een gegeven
moment een aparte naam aan is gegeven: Gaia
 .
.
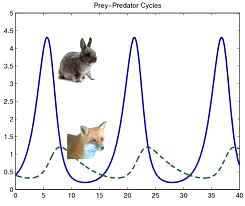 Maar
stel nu dat dit evenwicht verstoord wordt door één of andere externe invloed -
zeg er komt een clubje jagers langs en die schieten een flink deel van de vossen
dood. De konijnen kunnen zich meer vermenigvuldigen - zolang er voldoende gras is.
Maar, de jagers zijn inmiddels weer verder getrokken, dan komt er dus veel te
eten voor de overgebleven vossen, die zich ook snel gaan vermenigvuldigen. Tot
aan het punt dat er zo veel zijn dat ze de konijnen dreigen uit te roeien.
Enzovoort. Deze situatie is niet verzonnen, maar bij vossen en konijnen en vele
andere plaatsen in de natuur waar te nemen - en dientengevolge is deze situatie
ook veel bestudeerd. De grafiek rechts laat het resultaat van zo'n studie zien:
oscillaties in de aantallen vossen en konijnen. Een wijdverspreid verschijnsel.
Als het gaat om zaken van economische vraag-en-aanbod, heet het de varkenscyclus Maar
stel nu dat dit evenwicht verstoord wordt door één of andere externe invloed -
zeg er komt een clubje jagers langs en die schieten een flink deel van de vossen
dood. De konijnen kunnen zich meer vermenigvuldigen - zolang er voldoende gras is.
Maar, de jagers zijn inmiddels weer verder getrokken, dan komt er dus veel te
eten voor de overgebleven vossen, die zich ook snel gaan vermenigvuldigen. Tot
aan het punt dat er zo veel zijn dat ze de konijnen dreigen uit te roeien.
Enzovoort. Deze situatie is niet verzonnen, maar bij vossen en konijnen en vele
andere plaatsen in de natuur waar te nemen - en dientengevolge is deze situatie
ook veel bestudeerd. De grafiek rechts laat het resultaat van zo'n studie zien:
oscillaties in de aantallen vossen en konijnen. Een wijdverspreid verschijnsel.
Als het gaat om zaken van economische vraag-en-aanbod, heet het de varkenscyclus
 (Wikipedia). Ook de economie als geheel lijkt eraan onderhevig , onder de noemer
Kondratieff-golf
(Wikipedia). Ook de economie als geheel lijkt eraan onderhevig , onder de noemer
Kondratieff-golf
 (Wikipedia).
(Wikipedia).
Deze veelvoorkomende situaties zijn dus duidelijk van dezelfde vorm
als die van het gewichtje aan de veer dat je een zet geeft. Het is wiskundig
aantoonbaar dat golfverschijnselen horen bij evenwichtssituaties. Naarmate de
golven beter lijken om de mooie "sinussen" van een veer, is het
krachtenevenwicht simpeler - voor een zuivere sinus-golf is het aantal relevante
krachten twee.
De essentiële les van al dit voorgaande is dat talloze ingewikkeld lijkende
situaties ook met de meer simpele modellen afkomstig uit de natuurkunde
beschreven kunnen worden. En
wel omdat het beide soort gevallen om evenwichtssituaties gaat, de manier waarop
deze tot stand komen, en de manier waarop ze reageren op verstoringen van buiten
en van binnen.De algemene regels die hieruit gedestilleerd kunnen worden voor
de menswetenschappen in het algemeen zijn geformuleerd in Menswetenschappen, regels  .
Dit is praktisch het verst uitgewerkt wat betreft de menswetenschap die het
makkelijkst gekwantificeerd kan worden: de economie, zie Basis, economie I .
Dit is praktisch het verst uitgewerkt wat betreft de menswetenschap die het
makkelijkst gekwantificeerd kan worden: de economie, zie Basis, economie I
 en verder. Wat ook het meest direct blijkt in de economie dat het betrekkelijk
weinig moeite kost om simpele regels ervoor te formuleren
en verder. Wat ook het meest direct blijkt in de economie dat het betrekkelijk
weinig moeite kost om simpele regels ervoor te formuleren
 . De reden dat dit niet gebeurt, zowel in de economie als de sociologie, is dat
degenen die er professioneel in werkzaam zijn, gevestigde belangen hebben om dat
niet te doen, zowel als individu of als groep - in beide gevallen natuurlijk
gaande over eigenbelang. In het geval van economen is dat een materieel
eigenbelang
. De reden dat dit niet gebeurt, zowel in de economie als de sociologie, is dat
degenen die er professioneel in werkzaam zijn, gevestigde belangen hebben om dat
niet te doen, zowel als individu of als groep - in beide gevallen natuurlijk
gaande over eigenbelang. In het geval van economen is dat een materieel
eigenbelang 
 , leidende tot een stroom aan "fouten"
, leidende tot een stroom aan "fouten"
 , en voor sociologen een denkmatig eigenbelang
, en voor sociologen een denkmatig eigenbelang
 , leidende tot een even grote stroom fouten
, leidende tot een even grote stroom fouten

 .
.
Naar Evolutie
 , of
site home
, of
site home
 ·. ·.
|