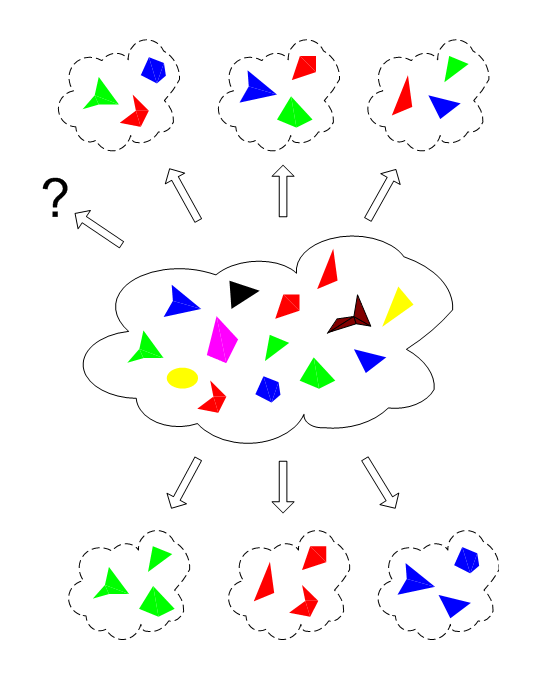
The world of reality

For triangles one may substitute cows, for quadrangles horses, etcetera. The various shapes and colors of the triangles represent the various individual traits of every cow, or horse, etcetera.

Reality itself already groups many individual objects into collections having common traits, as is denoted by a term like "cows'', and most aptly demonstrated by the existence of a "herd": in our perception it exists of many similar things (though not in those of the cows, of course).

But most groupings are hidden to our eyes, or to our direct perceptions. The discovery of these hidden groupings is the subject of science.

Two examples of groupings have been given below and above.

Please note that in choosing a symbolic representation of objects from reality, none of the at this point common choices of circles and squares have been used. This is done on purpose, because circles and squares are ideals that do not occur in reality. Houses have walls that are approximately perpendicular to the floor, and never exactly perpendicular.

In this context circles and squares are used to denote constructions of the mind, that can have ideal properties.

Aggregate 1 of objects from reality

Method: classification by color.

Color: green

Aggregate 1 of objects from reality

Method: classification by color.

Color: red

Aggregate 1 of objects from reality

Method: classification by color.

Color: blue

Aggregate 2 of objects from reality

Method: classification by the number of corners or sides

Number: five

Aggregate 2 of objects from reality

Method: classification by the number of corners or sides

Number: four

Aggregate 2 of objects from reality

Method: classification by the number of corners or sides

Number: three

Other aggregates of objects from reality

Method: As yet unknown.

The first big problem facing science is to find aggregates that are useful for further investigation and classification. The classification by color has been proven not to be very useful, the best known application being probably the rule that "red signifies danger".

The classification by the number of corners did prove to be useful in mathematics, as will be shown in the next figure. In the real world example of cows and horses this stands for the classification by species. Its usefulness lies in the fact that it was the basis for the idea of the genetic origin of the diversity found in the collection of species (as found by Mendel and his successors).

Determine a grouping of objects taken from reality

Method: Obviousness, eexperience, intuition, or the best guess.

Most of the presently known groups i.e. abstractions taken from reality, are based upon obviousness, like "cows", "horses", etcetera. This is because nature itself operates using these groups, also known as "species". Etcetera.

The human mind can make up abstractions for itself, which may or may not be as efficient as those of nature are. Predictions about their effectivity are difficult. The examples given in this geometrical model are those of grouping by color and of grouping by number of edges. The second turns out to be more effective than the first, as far as the capacity of building even more abstractions is concerned.

More details about the process of constructing natural groupings and abstractions is given here . This takes the process a step further back into reality by involving neurology, and is almost indispensible for further unerstanding of the workings of the human mind.

Determine a grouping of objects taken from reality

Method: Obviousness, eexperience, intuition, or the best guess.

Most of the presently known groups i.e. abstractions taken from reality, are based upon obviousness, like "cows", "horses", etcetera. This is because nature itself operates using these groups, also known as "species". Etcetera.

The human mind can make up abstractions for itself, which may or may not be as efficient as those of nature are. Predictions about their effectivity are difficult. The examples given in this geometrical model are those of grouping by color and of grouping by number of edges. The second turns out to be more effective than the first, as far as the capacity of building even more abstractions is concerned.

More details about the process of constructing natural groupings and abstractions is given here . This takes the process a step further back into reality by involving neurology, and is almost indispensible for further unerstanding of the workings of the human mind.