The world of abstractions

Aggregate 1 of abstraction of level 2

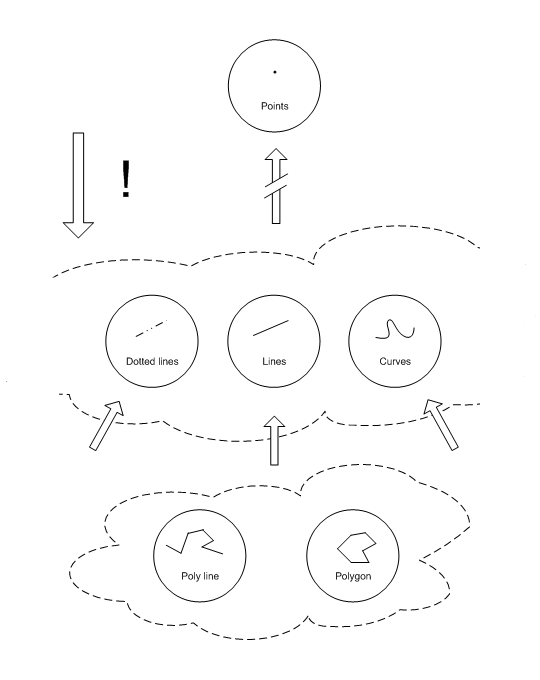
Method: Besides the level 2 abstraction "polygon", one can find other level 2 abstractions (not done explicitly here), with the "poly line" given as a (more or less fictional) example.

The next level is at this point is represented by the arrow pointing upwards.

The world of abstractions

Abstraction level 3

From the second order abstractions "polygon" and "poly line" one can construct a new abstraction, that of the general collection of (drawn) lines, abbreviated into "drawn lines".

The world of abstractions

Aggregate 1 of abstraction of level 3

Method: Besides the abstraction of "drawn lines", one can find abstractions of "dotted lines", "curved lines", etcetera.

The world of abstractions

Abstractions of level 4 and higher

In theory there is no limit to the number of levels of abstraction. In practice one sooner or later reaches a level after which higher levels serve no practical purpose.

The world of abstractions

The ladder of abstractions: the lessons.

Mathematicians also have tried to traverse the reverse path: constructing lines etcetera out of points. This has turned out to be a difficult job, due to the fact that in order to make something with a definite size out of something with no size at all, one has to have at least an infinite number of the size-less entities (there are also numbers that are more than infinity, called infinity times infinity, which can also be repeated an infinite number of times, etcetera)

The fact that the reverse path is so difficult, points towards the conclusion that in going the forward route, that we seem to have passed without too much effort, there are also problems hidden behind the bushes. If takes that much effort to build lower abstractions from higher ones, we apparently throw away characteristics that are quite essential to the lower abstractions, when getting to the higher ones.

The first lesson from this is that it is highly important to always test the conclusions drawn form your new abstractions, by going back to the lower abstractions - i.e. by going down the abstraction ladder again.

So the general rules of abstractions are:
The more abstract an entity, to the more other, lower, abstractions and objects it applies (from higher up this upside-down tree, one reaches more branches and leaves below).
The more abstract an entity, the smaller the importance of its aspect in the lower abstractions applies to (the higher the abstraction, the more has been left out; example: the fact that Bessie the cow exists out of molecules is quite irrelevant to her individual character).

The world of abstractions

Abstractions of level 4 and higher

In the field of mathematics one quickly arrives at the highest abstraction, being that of the "point" abstraction. The "point" is the abbreviation of something without any size, dimensions or characteristics - the ultimate abstraction.