Normale of Gaussiaanse verdeling
In Generalisties, menselijk
 kwam naar voren dat indien komende
op de ladder der structuren bij de meer omvangrijke zaken, in de natuurkunde
aangeduid als "macroscopisch" oftewel "je kan ze zien", de bijna
absoluutheid van categorieën als "atoom", "molecuul" enzovoort verdwijnt en
er steeds vagere grenzen ontstaan. Iets dat in de dagelijkse ervaring al bekend
is in de vorm dat de meeste, zo niet alle, menselijke eigenschappen
in variërende mate voorkomen, en even bekend is de manier waarop dat gebeurt: de meeste mensen zitten rond het
gemiddelde, en naarmate je verder van het gemiddelde afzit, zijn er minder
mensen met die eigenschap: mensen van 1,75 meter zijn heel gewoon, en die van
1,20 of 2,20 meter zijn zeldzaam, met allerlei variaties daartussen.
Mede vanwege het vele voorkomen ervan noemt men dit de "normale verdeling". kwam naar voren dat indien komende
op de ladder der structuren bij de meer omvangrijke zaken, in de natuurkunde
aangeduid als "macroscopisch" oftewel "je kan ze zien", de bijna
absoluutheid van categorieën als "atoom", "molecuul" enzovoort verdwijnt en
er steeds vagere grenzen ontstaan. Iets dat in de dagelijkse ervaring al bekend
is in de vorm dat de meeste, zo niet alle, menselijke eigenschappen
in variërende mate voorkomen, en even bekend is de manier waarop dat gebeurt: de meeste mensen zitten rond het
gemiddelde, en naarmate je verder van het gemiddelde afzit, zijn er minder
mensen met die eigenschap: mensen van 1,75 meter zijn heel gewoon, en die van
1,20 of 2,20 meter zijn zeldzaam, met allerlei variaties daartussen.
Mede vanwege het vele voorkomen ervan noemt men dit de "normale verdeling".
De wiskunde van de normale verdeling is ontdekt via wat achteraf de
"discrete benadering" kan worden genoemd: de normale verdeling is een continu
verschijnsel met het probleem: waar trek je de grenzen? Tegenwoordig, in het tijdperk van de computers en de
snelle berekeningen, hakt men dergelijke problemen bij voorkeur is stukjes
met constante waarden omdat dat makkelijk rekenen is, en benadert het
continue geval door de stukjes steeds kleiner te maken.
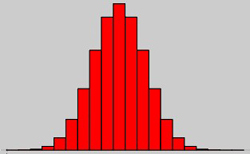 In
het geval van de normale verdeling gebeurt dat automatisch als gebruik maakt
van "experimenten" die vaste uitkomsten leveren zoals het Galton board
of het gooien van dobbelstenen. Want vaste uitkomsten per worp: 1 tot en met
6 voor één dobbelsteen, 2 tot en met 12 voor twee, enzovoort. En iedereen
weet al: met twee dobbelstenen zijn 2 en 12 zeldzaam, en 5, 6, en 7 veel
gewoner. En het gemiddelde wordt belangrijker naarmate je meer stenen neemt
en de verdeling ligt bij vier stenen wel redelijk duidelijk vast - voor een
tussenfase zie de grafiek rechts. In
het geval van de normale verdeling gebeurt dat automatisch als gebruik maakt
van "experimenten" die vaste uitkomsten leveren zoals het Galton board
of het gooien van dobbelstenen. Want vaste uitkomsten per worp: 1 tot en met
6 voor één dobbelsteen, 2 tot en met 12 voor twee, enzovoort. En iedereen
weet al: met twee dobbelstenen zijn 2 en 12 zeldzaam, en 5, 6, en 7 veel
gewoner. En het gemiddelde wordt belangrijker naarmate je meer stenen neemt
en de verdeling ligt bij vier stenen wel redelijk duidelijk vast - voor een
tussenfase zie de grafiek rechts.
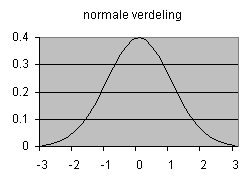 De
uiteindelijke continue verdeling, ook bekend onder de naam van de ontdekker
Gauss De
uiteindelijke continue verdeling, ook bekend onder de naam van de ontdekker
Gauss
 , en verkregen door steeds meer stenen te nemen
en te delen door het maximum, of met het Galton board: steeds kleinere
vakjes en steeds meer steeds kleinere knikkers, is weergeven rechts, tevens
"genormaliseerd" door te delen door het gemiddelde. Weerspiegelende het probleem "Bij zo'n verdeling, waar leg je de grenzen?"
Een probleem dat in de realiteit voortdurend op naargeestige wijze terugkeert bij bijvoorbeeld
schoolcijfers: bij welke totaalscore leg je de grens, en wat als iemand vlak
bij, meestal gaande over "onder", die grens zit?
, en verkregen door steeds meer stenen te nemen
en te delen door het maximum, of met het Galton board: steeds kleinere
vakjes en steeds meer steeds kleinere knikkers, is weergeven rechts, tevens
"genormaliseerd" door te delen door het gemiddelde. Weerspiegelende het probleem "Bij zo'n verdeling, waar leg je de grenzen?"
Een probleem dat in de realiteit voortdurend op naargeestige wijze terugkeert bij bijvoorbeeld
schoolcijfers: bij welke totaalscore leg je de grens, en wat als iemand vlak
bij, meestal gaande over "onder", die grens zit?
Er is dus een
behoefte aan min-of-meer objectiveerbare grenzen, en die wordt verschaft door
de wiskunde. Met als basis "gezond verstand".
Dat laatste kan men
halen uit de genoemde schoolcijfers. Waar het in eerste instantie om gaat,
zijn de gemiddeldes: gemiddelde van alle leerlingen een 7? Dan "goede
leerlingen", "goede leraren","goede school". Of in diverse combinaties. De
wiskundige notatie voor de berekening van het gemiddelde is (voor uitleg van
die notatie, zie hier
 ):
Maar dat gemiddelde van 7 kan op oneindige veel manieren tot stand
komen. Iedere leerling een 7, is uiterst onwaarschijnlijk, weet iedereen.
Volgende mogelijkheid: de helft een 6 en de helft een 8. Hoe druk je dit
verschil uit? ):
Maar dat gemiddelde van 7 kan op oneindige veel manieren tot stand
komen. Iedere leerling een 7, is uiterst onwaarschijnlijk, weet iedereen.
Volgende mogelijkheid: de helft een 6 en de helft een 8. Hoe druk je dit
verschil uit?
De methode is als volgt: trek van ieder cijfer het
gemiddelde af (7), dat is de individuele afwijking. Tel dit bij elkaar op en
deel door het aantal leerlingen. Uitkomst in het eerste geval: 0. Zoals je
wilt. Uitkomst in het tweede geval: ook 0. Vervelend.
Die tweede nul
komt door deze optelling, als het over tien leerlingen met 6 en 8 gaat: -1 -
1 - 1 - 1 - 1 + 1 + 1 + 1 + 1 + 1 = 0. Kortom: die minnen moeten weg. Zonder
die minnen is de afwijking na delen door het aantal: 1. Precies wat het
gezonde verstand zegt: ze wijken allemaal 1 van het gemiddelde af.
De
wiskundige methode voor het verwijderen van de minnen is eerst kwadrateren en dan wortel trekken:
De totale afwijking voor alle leerlingen uit een klas:
Oftewel: de gewogen afwijking (die per leerling) is:
Wat heet de standaarddeviatie σ en hergeschreven kan worden als:
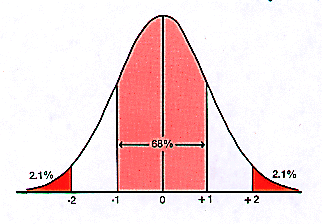 Deze berekening kan je loslaten op een verzameling scores die willekeurig
verdeeld zijn, dat wil zeggen: die tezamen een Gaussverdeling vormen. Dat
levert dus een gemiddelde afwijking van het gemiddelde. Oftewel: wie
daaronder valt wijkt minder dan gemiddeld af - en daarboven dus meer. Dus
dat is een maatstaf voor hoe ver een score van het gemiddelde afwijkt. Een
formulering die intuïtief klopt. Met een uitkomst die intuïtief klopt, zie
de grafiek rechts waarin de verdeling zodanig is dat het gemiddelde 0 is, en
de scores aangeven hoeveel ze van het gemiddelde afwijken. De uitkomst: circa tweederde van alle gevallen ligt
tussen de twee punten die één maal de
standaarddeviatie van het gemiddelde afliggen, het licht rode gebied in de
grafiek, en circa 95 procent van alle gevallen ligt tussen de punten die meer twee
maal de standaarddeviatie van het gemiddelde afliggen, wat betekent dat slechts
circa 5 procent erbuiten ligt, het rode deel van de grafiek.
Deze berekening kan je loslaten op een verzameling scores die willekeurig
verdeeld zijn, dat wil zeggen: die tezamen een Gaussverdeling vormen. Dat
levert dus een gemiddelde afwijking van het gemiddelde. Oftewel: wie
daaronder valt wijkt minder dan gemiddeld af - en daarboven dus meer. Dus
dat is een maatstaf voor hoe ver een score van het gemiddelde afwijkt. Een
formulering die intuïtief klopt. Met een uitkomst die intuïtief klopt, zie
de grafiek rechts waarin de verdeling zodanig is dat het gemiddelde 0 is, en
de scores aangeven hoeveel ze van het gemiddelde afwijken. De uitkomst: circa tweederde van alle gevallen ligt
tussen de twee punten die één maal de
standaarddeviatie van het gemiddelde afliggen, het licht rode gebied in de
grafiek, en circa 95 procent van alle gevallen ligt tussen de punten die meer twee
maal de standaarddeviatie van het gemiddelde afliggen, wat betekent dat slechts
circa 5 procent erbuiten ligt, het rode deel van de grafiek.
Dit heeft directe praktische toepassing voor bijvoorbeeld de schoenenfabrikant. Welke maten moet de
fabrikant in zijn assortiment hebben om zo veel mogelijk klanten te bedienen,
zonder te veel geld kwijt te zijn aan de extreme gevallen waarvan hij heel
weinig verkoopt. Dit wordt volledig bepaald door de standaarddeviatie. Wil hij
95 procent van alle mensen bedienen, dan moet hij de gemiddelde maat nemen, en
twee standaarddeviaties daarboven en daarbeneden maken. En voor andere
percentages valt dat allemaal precies te berekenen.
Conclusie: ook voor
volkomen willekeurige verdelingen vallen grenzen af te spreken. Dus ook bij
volkomen willekeurige verdeling kunnen er generalisaties worden gemaakt -
zeg de groep van alle normale gevallen (deviatie kleiner dan 1
standaarddeviatie), de uitzonderlijke gevallen (deviatie tussen 1 en 2
standaarddeviatie), en de afwijkende gevallen (deviatie groter dan 2). De
eerste twee kan je structureel afhandelen - bijvoorbeeld door een indeling
in vmbo, mbo, hbo en universiteit - of de "confectiematen" in de winkel. De
tweede groep kan je alleen op individuele basis afhandelen: het speciale
onderwijs - of de gevallen voor de schoenmaker-vakman.
De genoemde
praktische voorbeelden laten zien dat zelfs voor volkomen willekeurige
verdeling, de wensen en noodzaken van de maatschappelijke praktijk al tot
eindeloos veel generalisaties hebben geleid. En dat generalisaties de kern
vormen van het inrichten van een maatschappij. Waarbij voor de volkomen
willekeurige verdeling gewoon rekening gehouden wordt met de vaagheid van de
grenzen ervan. Een proces dat door heel veel politici en beleidsmakers
verkeerd gehanteerd wordt
 .
.
Maar het bovenstaande is het meest willekeurige geval. Er zijn zeer veel maatschappelijke zaken die van meerdere parameters
afhangen. De vraag is dan: hangen die samen of niet? Als ze samenhangen,
wordt de verdeling scherper, zie het volgende onderwerp: combinaties
 . .
Naar Psychosociohistorie, inleiding
 , of site home , of site home
 ·. ·.
|
 .
.
 In
het geval van de normale verdeling gebeurt dat automatisch als gebruik maakt
van "experimenten" die vaste uitkomsten leveren zoals het Galton board
of het gooien van dobbelstenen. Want vaste uitkomsten per worp: 1 tot en met
6 voor één dobbelsteen, 2 tot en met 12 voor twee, enzovoort. En iedereen
weet al: met twee dobbelstenen zijn 2 en 12 zeldzaam, en 5, 6, en 7 veel
gewoner. En het gemiddelde wordt belangrijker naarmate je meer stenen neemt
en de verdeling ligt bij vier stenen wel redelijk duidelijk vast - voor een
tussenfase zie de grafiek rechts.
In
het geval van de normale verdeling gebeurt dat automatisch als gebruik maakt
van "experimenten" die vaste uitkomsten leveren zoals het Galton board
of het gooien van dobbelstenen. Want vaste uitkomsten per worp: 1 tot en met
6 voor één dobbelsteen, 2 tot en met 12 voor twee, enzovoort. En iedereen
weet al: met twee dobbelstenen zijn 2 en 12 zeldzaam, en 5, 6, en 7 veel
gewoner. En het gemiddelde wordt belangrijker naarmate je meer stenen neemt
en de verdeling ligt bij vier stenen wel redelijk duidelijk vast - voor een
tussenfase zie de grafiek rechts. De
uiteindelijke continue verdeling, ook bekend onder de naam van de ontdekker
Gauss
De
uiteindelijke continue verdeling, ook bekend onder de naam van de ontdekker
Gauss
 Deze berekening kan je loslaten op een verzameling scores die willekeurig
verdeeld zijn, dat wil zeggen: die tezamen een Gaussverdeling vormen. Dat
levert dus een gemiddelde afwijking van het gemiddelde. Oftewel: wie
daaronder valt wijkt minder dan gemiddeld af - en daarboven dus meer. Dus
dat is een maatstaf voor hoe ver een score van het gemiddelde afwijkt. Een
formulering die intuïtief klopt. Met een uitkomst die intuïtief klopt, zie
de grafiek rechts waarin de verdeling zodanig is dat het gemiddelde 0 is, en
de scores aangeven hoeveel ze van het gemiddelde afwijken. De uitkomst: circa tweederde van alle gevallen ligt
tussen de twee punten die één maal de
standaarddeviatie van het gemiddelde afliggen, het licht rode gebied in de
grafiek, en circa 95 procent van alle gevallen ligt tussen de punten die meer twee
maal de standaarddeviatie van het gemiddelde afliggen, wat betekent dat slechts
circa 5 procent erbuiten ligt, het rode deel van de grafiek.
Deze berekening kan je loslaten op een verzameling scores die willekeurig
verdeeld zijn, dat wil zeggen: die tezamen een Gaussverdeling vormen. Dat
levert dus een gemiddelde afwijking van het gemiddelde. Oftewel: wie
daaronder valt wijkt minder dan gemiddeld af - en daarboven dus meer. Dus
dat is een maatstaf voor hoe ver een score van het gemiddelde afwijkt. Een
formulering die intuïtief klopt. Met een uitkomst die intuïtief klopt, zie
de grafiek rechts waarin de verdeling zodanig is dat het gemiddelde 0 is, en
de scores aangeven hoeveel ze van het gemiddelde afwijken. De uitkomst: circa tweederde van alle gevallen ligt
tussen de twee punten die één maal de
standaarddeviatie van het gemiddelde afliggen, het licht rode gebied in de
grafiek, en circa 95 procent van alle gevallen ligt tussen de punten die meer twee
maal de standaarddeviatie van het gemiddelde afliggen, wat betekent dat slechts
circa 5 procent erbuiten ligt, het rode deel van de grafiek.