Interactie, detail
In Individu, groep, en interactie
 is aan het basale gedrag van groepen onafhankelijke zaken of individuen
is aan het basale gedrag van groepen onafhankelijke zaken of individuen
 het verschijnsel van interactie toegevoegd. Dat is daar ruwweg opgesplitst
in twee soorten: "sterk" en "zwak", waarbij "sterk" omschreven is als
"leidende tot binding in nieuwe groepen die zwakkere interactie hebben".
Waarbij "zwak"gedefineerd is als klein ten opzichte van de ook bestaande
invloeden die de elementen uit elkaar drijven of anderszins onafhankelijk
maken, waarvan twee voorbeelden zijn gegeven: de door de mens gemaakte
dobbelstenen die zich helemaal los van elkaar willekeurig kunnen bewegen, en
de willekeurige bewegingen van de moleculen in een gas ten gevolge van de
temperatuur. En met wiskunde kan aangetoond worden dat deze twee eigenlijk
hetzelfde zijn: middels de statistiek van de willekeur. Door zwakke interactie
("magneetjes in de dobbelstenen") krijg je kleine verstoringen van dit
patroon, door sterke interactie ("superlijm op de dobbelstenen") gaan de
elementen aan elkaar plakken en gaan de voorgaande regels op voor de nieuwe
basiselementen.
het verschijnsel van interactie toegevoegd. Dat is daar ruwweg opgesplitst
in twee soorten: "sterk" en "zwak", waarbij "sterk" omschreven is als
"leidende tot binding in nieuwe groepen die zwakkere interactie hebben".
Waarbij "zwak"gedefineerd is als klein ten opzichte van de ook bestaande
invloeden die de elementen uit elkaar drijven of anderszins onafhankelijk
maken, waarvan twee voorbeelden zijn gegeven: de door de mens gemaakte
dobbelstenen die zich helemaal los van elkaar willekeurig kunnen bewegen, en
de willekeurige bewegingen van de moleculen in een gas ten gevolge van de
temperatuur. En met wiskunde kan aangetoond worden dat deze twee eigenlijk
hetzelfde zijn: middels de statistiek van de willekeur. Door zwakke interactie
("magneetjes in de dobbelstenen") krijg je kleine verstoringen van dit
patroon, door sterke interactie ("superlijm op de dobbelstenen") gaan de
elementen aan elkaar plakken en gaan de voorgaande regels op voor de nieuwe
basiselementen.
 Dan kan je nog steeds de vraag stellen of het niet
mogelijk is om interacties te hebben van een tussensoort, die je
"middelsterk" zou kunnen noemen - uit te breiden tot een heel continuüm van
sterktes. Het antwoord daarop was dat dat in de levende natuur, waar je een
continuüm van alle
mogelijke uitingen van levensvormen zou kunnen verwachten, de werkelijkheid is
dat ze door de natuur "geschikt" is in vele stammen, rassen, geslachten,
enzovoort die duidelijk onderscheidbaar zijn. Met overgangsvormen die
meestal van dusdanig korte levensduur en daardoor zo zeldzaam vindbaar zijn
dat ze alom bekend zijn als de "missing links" - rechts een
afbeelding van het zeldzame fossiel van een archeopterix, de "vliegende
dinosaurus" die missing link is/was naar de vogels. Dan kan je nog steeds de vraag stellen of het niet
mogelijk is om interacties te hebben van een tussensoort, die je
"middelsterk" zou kunnen noemen - uit te breiden tot een heel continuüm van
sterktes. Het antwoord daarop was dat dat in de levende natuur, waar je een
continuüm van alle
mogelijke uitingen van levensvormen zou kunnen verwachten, de werkelijkheid is
dat ze door de natuur "geschikt" is in vele stammen, rassen, geslachten,
enzovoort die duidelijk onderscheidbaar zijn. Met overgangsvormen die
meestal van dusdanig korte levensduur en daardoor zo zeldzaam vindbaar zijn
dat ze alom bekend zijn als de "missing links" - rechts een
afbeelding van het zeldzame fossiel van een archeopterix, de "vliegende
dinosaurus" die missing link is/was naar de vogels.
 Er
zijn wel meer tussenvormen, bedacht door de menselijke fantasie: de eenhoorn, het
vliegende paard, enzovoort. Waarop voor het gebrek aan levensvatbaarheid
ervan de "gezond verstand"-regel van Goethe van toepassing is: "Je hoeft
niet in China geweest te zijn om te weten dat de lucht daar ook blauw is".
In dit geval bestaande uit de onbewuste kennis dat de vereisten om op het
land een hoge snelheid gecombineerd met een hoge massa te kunnen halen
("paard"),
volkomen in strijd zijn met de eisen om het luchtruim te kunnen kiezen
("vogel"). Voor
de natuur. Er
zijn wel meer tussenvormen, bedacht door de menselijke fantasie: de eenhoorn, het
vliegende paard, enzovoort. Waarop voor het gebrek aan levensvatbaarheid
ervan de "gezond verstand"-regel van Goethe van toepassing is: "Je hoeft
niet in China geweest te zijn om te weten dat de lucht daar ook blauw is".
In dit geval bestaande uit de onbewuste kennis dat de vereisten om op het
land een hoge snelheid gecombineerd met een hoge massa te kunnen halen
("paard"),
volkomen in strijd zijn met de eisen om het luchtruim te kunnen kiezen
("vogel"). Voor
de natuur.
Maar hoe waar ook: intuïtie is toch een onbevredigend antwoord
gezien vanuit het rationele verstand, aangezien je graag zou willen weten
wat de regels zijn die achter die intuïtie steken, al was het maar omdat dat
je een mogelijkheid zou kunnen bieden om ze te omzeilen.
En achter de
splitsing in sterke en zwakke interactie zitten wel degelijk aanwijsbare
factoren.
Om dit aan te tonen moet weer een beroep gedaan worden op
de natuurkunde, om twee verwante redenen: de natuurkunde is het enige vak
dat tot nu toe geslaagd is in dit soort aanpak, en omdat als je vraagt om een
verklaring, je altijd dieper moet gaan dan het vak waarbinnen je de vraag
stelt: de vraag naar "Hoe?" stel je binnen het vak, de vraag naar "Waarom?"
aan het vak eronder.
En de vraag luidde: Waarom zijn op het niveau
van dobbelstenen en moleculen er voornamelijk of alleen "sterke" en "zwakke"
interactie, maar nauwelijks of niet ertussenin? En let op: dit gaat
natuurlijk terugkomen in de vakken erboven, zoals biologie, neurologie,
psychologie, en sociologie. Misschien niet keihard, maar wel op essentiële
wijze.
Voor degenen die graag van tevoren de uitslag kennen: de
antwoorden luiden "Het Periodiek Systeem der Elementen", en "de quantummechanica". En bij beide komt, om de
invloed ervan te snappen, geen enkele
wiskunde aan te pas.
"Het Periodiek Systeem der Elementen" heeft geen
naam en bekende ontdekker, zoals "Coulomb-wet" en "Van der Waals-kracht",
omdat die ontdekker een Rus was (Mendelejev), en Russen zijn de vijand en
willen we niet kennen (dat is een ander onderwerp genaamd "De Strijd tussen
Residentie en Nomadisme" en ook wel "De Koude Oorlog"). Onderstaand is een
versie met de
op deze plek noodzakelijke details, in een vorm die niet gevonden kon worden
op het internet (op tientallen miljoenen bestaande "hits") - deze versie
komt uit The Reflexive Universe (1976) van Arthur M. Young
 , en
geeft de eerste drie rijen van het systeem: , en
geeft de eerste drie rijen van het systeem:
Wat hier getoond wordt, is dat atomen voorkomen in rijen waarin het
aantal elektronen toeneemt, van links 1 tot rechts 7, en dat bij een aantal
van 8 hoger dit zich herhaalt, waarbij die 8 erbij niet mee lijken te
tellen. Die eerdere 8 zijn in de tweede rij voorgesteld met behulp van een
cirkeltjes onder de buitenste elektronen. Bij het geval van 8 (2 bij alleen
de eerste) elektronen aan de
buitenkant is de ruimte kennelijk op, want dan begint het tellen opnieuw, in
een baan verder van de kern. Deze atomen, helium, neon, argon, enzovoort,
hebben nauwelijks tot
niet last van interactie, en staan bekend staan als de edelgassen.
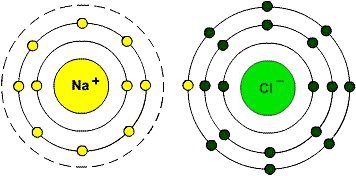 Al deze atomen zijn elektrisch neutraal,
dus zouden geen last hebben van sterke interactie, zou je zeggen. Dat werkt
anders. In werkelijkheid is het zo dat 8 elektronen in de buitenste schil als
"neutraal" worden gezien - atomen met 1, 2, of 3 elektronen in de buitenste
schil staan die elektronen makkelijk af aan atomen die 1, 2 of 3 elektronen
te weinig hebben, ten opzichte van 8, in de buitenste schil. Dus natrium, of
in het Engels "sodium", met 1 elektron aan de buitenkant, combineert graag
met chloor ("chlorine"), met 1 elektron te kort - tot een stof die
overbekend is als "zout" in de zin van tafelzout of "het zout in de zee".
Enzovoort. Al deze atomen zijn elektrisch neutraal,
dus zouden geen last hebben van sterke interactie, zou je zeggen. Dat werkt
anders. In werkelijkheid is het zo dat 8 elektronen in de buitenste schil als
"neutraal" worden gezien - atomen met 1, 2, of 3 elektronen in de buitenste
schil staan die elektronen makkelijk af aan atomen die 1, 2 of 3 elektronen
te weinig hebben, ten opzichte van 8, in de buitenste schil. Dus natrium, of
in het Engels "sodium", met 1 elektron aan de buitenkant, combineert graag
met chloor ("chlorine"), met 1 elektron te kort - tot een stof die
overbekend is als "zout" in de zin van tafelzout of "het zout in de zee".
Enzovoort.
Maar wat gebeurt er dan bij het aantal van 4 - precies op
de helft? Het antwoord bevindt zich in uw lichaam en hoofd en in uw
computer: dit is een dusdanig "wankele" situatie dat de natuur van de
mogelijkheden die dat biedt gebruik heeft gemaakt voor de ontwikkeling van
ingewikkelde moleculen tot zeer ingewikkelde moleculen tot moleculen die zichzelf
kunnen reproduceren - het leven. Voor het geval van koolstof ("carbon"). En
tot het geval van hypergevoelige en hyperkleine schakelaars te combineren in
de miljoenen tot de kern van computer. Voor het geval van silicium
("silicon").
Dit is dus de praktische illustratie van de eerder
geuite stelling: sterke interactie combineert net zo lang, tot er zwakke
interactie overblijft.
Maar waarom heeft het periodiek systeem die vorm
van rijen van 2, 8, enzovoort?
Het antwoord daarvan ligt in de
quantummechanica. Wat door (bijna) alle natuurkundigen als dusdanig moeilijk
wordt gezien dat
iedereen die het idee heeft dat het simpeler kan, door natuurkundigen voor
"gestoord" wordt versleten. Dus daarom hier wat "gestoorde" opmerkingen,
voor degenen die graag willen weten "Waarom?"
 Alles wordt een stuk
begrijpelijker, als je één veronderstelling doet: alle deeltjes bestaan uit,
naast hun massa en eventuele elektrische lading, ook uit een trilling. Een
veronderstelling in de moderne tijd als eerste gedaan door Louis de Broglie Alles wordt een stuk
begrijpelijker, als je één veronderstelling doet: alle deeltjes bestaan uit,
naast hun massa en eventuele elektrische lading, ook uit een trilling. Een
veronderstelling in de moderne tijd als eerste gedaan door Louis de Broglie
 . En
over trillingen is best heel veel bekend, want alle
muziekinstrumenten maken trillingen, uiteindelijk in de lucht die we dan geluid of een
meer specifiek "toon" of "noot" noemen, en iedereen weet hoe je de toon van een
muziekinstrument varieert: je moet de snaar of de luchtpijp of het
(trommel-)vel groter/langer en kleiner/korter maken: de afmeting bepaalt de toon. De
afmeting beperkt het soort trilling tot één enkele. Of beter: die ene enkele,
plus twee maal zo hoog, drie maal zo hoog, enzovoort - de boventonen. De
basistoon bepaalt de noot, de boventonen van welk instrument het komt: veel
hoge boventonen oftewel wel "schel": hobo of viool of iets dergelijks.
Rechtsboven het trillingspatroon van een cirkelvormige plaat, zeg een
bekkenhelft of een trommelvel, met naast de basistrilling diverse boventonen
(de kleinere patronen aan de binnenkant). . En
over trillingen is best heel veel bekend, want alle
muziekinstrumenten maken trillingen, uiteindelijk in de lucht die we dan geluid of een
meer specifiek "toon" of "noot" noemen, en iedereen weet hoe je de toon van een
muziekinstrument varieert: je moet de snaar of de luchtpijp of het
(trommel-)vel groter/langer en kleiner/korter maken: de afmeting bepaalt de toon. De
afmeting beperkt het soort trilling tot één enkele. Of beter: die ene enkele,
plus twee maal zo hoog, drie maal zo hoog, enzovoort - de boventonen. De
basistoon bepaalt de noot, de boventonen van welk instrument het komt: veel
hoge boventonen oftewel wel "schel": hobo of viool of iets dergelijks.
Rechtsboven het trillingspatroon van een cirkelvormige plaat, zeg een
bekkenhelft of een trommelvel, met naast de basistrilling diverse boventonen
(de kleinere patronen aan de binnenkant).
Dus: zodra je deeltjes als elektronen een trilling toekent, en ze hebben
maar een beperkte ruimte zoals wanneer ze rond een kern draaien, dan kunnen ze
slechts in een beperkt aantal trillingstoestanden voorkomen.
En dat
is de reden (met nog wat hier totaal onbelangrijke technische details die de
precieze getallen bepalen) dat atomen voorkomen in reeksen, waaronder die van 8
(2, 8, 18, ... om precies te zijn). Waar nog slechts één enkele
essentiële regel bij komt (van Wolfgang Pauli
 ):
twee elektronen kunnen niet in dezelfde trillingstoestand zitten. Iedere extra toegevoegde
móet in een "hogere" toestand dan de vorige. En zo ontstaan de boven- en
onderschillen. ):
twee elektronen kunnen niet in dezelfde trillingstoestand zitten. Iedere extra toegevoegde
móet in een "hogere" toestand dan de vorige. En zo ontstaan de boven- en
onderschillen.
Goed: er is nu een verklaring voor het "gat" tussen
sterke en zwakke interactie. En er zijn twee voorbeelden langsgekomen van de waarde van de
uitzonderingen: dan gebeuren er speciale dingen. De zaken zijn dan niet
simpel in de natuur, en de zaken die niet simpel zijn, bieden ruimte voor
nieuwe mogelijkheden.
Daarvan is er nog één geval dat essentieel is voor
sociologische toepassingen. Net als de al genoemde bevindt zich dat in
middengebieden in het periodiek systeem. Door het samenspel van de elektrische krachten en de krachten die leiden tot het verzamelen in
schillen, zijn er meerdere reeksen van atomen met halfgevulde onderschillen,
bijvoorbeeld 8 in plaats van 18. Die atomen hebben een redelijk sterke onderlinge
aantrekkingskracht, waardoor ze, in tegenstelling tot de echte sterk-interacterende atomen, zelfstandig voor kunnen komen in grote hoeveelheden, en
die bij de mens bekend staan als de "metalen". Van oudsher als eerste koper,
zilver, goud, tin, enzovoort, en wat later in de oerhistorie ook ijzer (dat moet je eerst uit
haar "erts" halen). Vanwege hun relatief sterke onderlinge aantrekking
reageren ze weinig met andere stoffen en met name weinig met zuurstof,
waarvan er veel in de atmosfeer zit, zodat ze niet "roesten" of oxideren tot
de bekende harde materialen als zand, mineralen, enzovoort (het meeste zand
is siliciumoxide, veel van de edelstenen zoals robijn en saffier bestaan uit
voornamelijk aluminiumoxide).
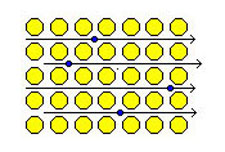 Het speciale aan metalen is dat
ze wel graag hun elektronen afstaan, maar omdat ze alleen te midden van
zichzelf zitten, doen ze dat dus niet aan elkaar, maar aan een algemene
toestand "in het midden", of beter: "ertussenin", in welke toestand die buitenste
elektronen vrij kunnen bewegen van het ene naar het andere atoom.
Natuurkundigen hebben zulke stoffen ook "geleiders" genoemd: de elektronen
kunnen vrij rondstromen, dus "lading" (van de elektronen) kan vrij
rondstromen, dus kan je een ladingsstroom sturen door een metaal. En
ladingstroom is wat de in de gewone wereld bekend staat als "stroom". En
omdat ze stroom geleiden, weerkaatsen ze het licht, waardoor ze glanzen, wat
mensen, en veel dieren, dan ook nog eens aantrekkelijk vinden. Dit
vermoedelijk onder het motto: licht is goed, veel licht is beter ...
(Of ... meer waarschijnlijk: door de gelijkenis met rijp en glanzend fruit). Het speciale aan metalen is dat
ze wel graag hun elektronen afstaan, maar omdat ze alleen te midden van
zichzelf zitten, doen ze dat dus niet aan elkaar, maar aan een algemene
toestand "in het midden", of beter: "ertussenin", in welke toestand die buitenste
elektronen vrij kunnen bewegen van het ene naar het andere atoom.
Natuurkundigen hebben zulke stoffen ook "geleiders" genoemd: de elektronen
kunnen vrij rondstromen, dus "lading" (van de elektronen) kan vrij
rondstromen, dus kan je een ladingsstroom sturen door een metaal. En
ladingstroom is wat de in de gewone wereld bekend staat als "stroom". En
omdat ze stroom geleiden, weerkaatsen ze het licht, waardoor ze glanzen, wat
mensen, en veel dieren, dan ook nog eens aantrekkelijk vinden. Dit
vermoedelijk onder het motto: licht is goed, veel licht is beter ...
(Of ... meer waarschijnlijk: door de gelijkenis met rijp en glanzend fruit).

 Maar er is nog een aantrekkelijke eigenschap aan metalen, die geen
andere soort stof bezit: ze zijn (relatief) makkelijk vervormbaar. En
daardoor te voorzien van scherpe uiteinden. Niet zo scherp als die van steen
die voorheen het gereedschap van de oermens waren, maar wel redelijk in de
buurt. En bovendien na het bot worden weer goed scherp te krijgen. En dat in
alle mogelijke afmetingen en vormen, en niet, zoals bij steen, uitsluitend
in klompen - je kan wel een zwaard maken van metaal, maar niet van steen. De
bruikbaarheid van steen ten opzichte van metaal als gereedschap is die van
de vuistbijl ten opzichte van het zwaard. Of misschien relevanter en zeker
vreedzamer: die van een stenen ploeg ten opzichte van één van ijzer. Want
hoe beter de landbouwtechniek, hoe hoger de voedselopbrengst, en hoe groter
en diverser de bevolkingssamenstelling. En hoe groter de specialisatie. En
hoe meer intellectuele ontwikkeling. En hoe hoger de beschaving. Maar er is nog een aantrekkelijke eigenschap aan metalen, die geen
andere soort stof bezit: ze zijn (relatief) makkelijk vervormbaar. En
daardoor te voorzien van scherpe uiteinden. Niet zo scherp als die van steen
die voorheen het gereedschap van de oermens waren, maar wel redelijk in de
buurt. En bovendien na het bot worden weer goed scherp te krijgen. En dat in
alle mogelijke afmetingen en vormen, en niet, zoals bij steen, uitsluitend
in klompen - je kan wel een zwaard maken van metaal, maar niet van steen. De
bruikbaarheid van steen ten opzichte van metaal als gereedschap is die van
de vuistbijl ten opzichte van het zwaard. Of misschien relevanter en zeker
vreedzamer: die van een stenen ploeg ten opzichte van één van ijzer. Want
hoe beter de landbouwtechniek, hoe hoger de voedselopbrengst, en hoe groter
en diverser de bevolkingssamenstelling. En hoe groter de specialisatie. En
hoe meer intellectuele ontwikkeling. En hoe hoger de beschaving.
Waarmee we automatisch al op het punt van de sociologie zijn beland.
Maar eerst een stapje terug, naar het eerst doel van dit artikel: laten
zien dat er verschillende soorten interacties zijn, en niet een heel
continuüm. Wat dus redelijkerwijs bewezen is voor de dode natuur, al eerder
gebleken is voor de evolutie binnen de levende natuur, en waarvan het dus
behoorlijk aannemelijk is dat het zich voortzet op hogere niveaus. De al
genoemde Arthur Young volgde een soortgelijke gedachtengang en heeft dit in
een soort "voortgezet periodiek systeem" gegoten:
Wat wel niet letterlijk is dat hier de bedoeling is, maar het idee
erachter wel overbrengt.
Wat dus ongeveer alle lagen betreft onder die van de mens
Waarmee overgegaan kan worden tot de
vertaling van diverse van de geïntroduceerde begrippen naar zaken die
concreet toegepast kunnen worden in de sociologie. Van belang is:
- dat er qua sterkte redelijk te onderscheiden
soorten interacties zijn.
- dat voor het beschrijven van de toestand van
een systeem, er minimaal twee soorten interactie nodig zijn: een
aantrekkende en een van elkaar bewegende - met uitsluitend één van de twee
resulteert chaos (de tweede) of een zwart gat (de eerste).
- dat er qua
resulterende effecten voor factoren als "hardheid", "flexibiliteit",
diversiteit", en "duurzaamheid" of "overlevingswaarde" verschillende soorten
interacties zijn.
- dat de meest diverse, flexibele, en
overlevenskrachtige vormen van interactie die zijn die middelmatig sterk
zijn, en een grote mate van onderlinge "samenwerking" vertonen - in de
praktijk: die van halfvolle atomen en metalen.
Dat laatste is dus een
gevolg van de al eerste gedane observatie: sterke interactie kweekt gewoon
nieuwe eenheden, tot er zwakke interactie overblijft. En zwakke interactie
lijkt te veel op gewoon willekeurig en Gaussiaans gedrag
 om iets echt zinvol nieuws te kunnen voortbrengen. De simpele dode natuur
blijft de simpele dode natuur.
om iets echt zinvol nieuws te kunnen voortbrengen. De simpele dode natuur
blijft de simpele dode natuur.
Op welk punt hier ook de vraag gesteld
kan worden welke bekende vormen van sociale interactie en gedrag
overeenkomen met welke soorten van natuurkundige interactie. Dat ligt
eigenlijk zo voor de hand, dat invullen ervan overbodig zou moeten zijn.
Voor de volledigheid: alle cultuur die voornamelijk bouwt op vaststaande
regels, komt overeen met harde interactie. Alle cultuur die voornamelijk
bouwt op "geen regels", komt overeen met zwakke interactie. En culturen die
voornamelijk bouwen op middelmatig-harde maar toch flexibele regels, zijn de
culturen met veruit de meeste flexibiliteit, diversiteit, en
overlevingswaarde.
De eerste soort wordt ingevuld door alle
religies
 (met mogelijkerwijs een uitzondering maar die is hier niet bekend) en alle
vormen van ideologie
(met mogelijkerwijs een uitzondering maar die is hier niet bekend) en alle
vormen van ideologie
 (met voor sommige ervan wat minder hardheid in dat ze zonder al te veel
schade kunnen verdwijnen), de tweede door alle vormen van nomadisme
(met voor sommige ervan wat minder hardheid in dat ze zonder al te veel
schade kunnen verdwijnen), de tweede door alle vormen van nomadisme
 zoals die van de Roma
zoals die van de Roma
 en
de Joden en
de Joden
 ,
en de derde door de westerse en Aziatische culturen ,
en de derde door de westerse en Aziatische culturen
 . Voor alle concreet genoemden in diverse mate.
. Voor alle concreet genoemden in diverse mate.
Vanaf dit punt kan
overgegaan worden naar concrete toepassingen van het interactiemodel. Op dit
moment is dit op deze website al gedaan
voor het geval van menging van culturen hier
 -
dit levert uitkomsten die volstrekt in overeenstemming zijn met de
waargenomen verschijnselen. Verdere concrete voorbeelden ontbreken nog. -
dit levert uitkomsten die volstrekt in overeenstemming zijn met de
waargenomen verschijnselen. Verdere concrete voorbeelden ontbreken nog.
Op meer theoretisch vlak zijn een aantal van de genoemde begrippen over
te nemen uit het interactiemodel al vertaald naar een meer complete verzameling regels voor de menswetenschappen en
met name de sociologie hier
 .
Mogelijkerwijs wordt dit interactieverhaal in de toekomst verder aangevuld. .
Mogelijkerwijs wordt dit interactieverhaal in de toekomst verder aangevuld.
Naar Psychosociohistorie, inleiding
 , of
site home , of
site home
 . .
|