Formalisme: stromen, natuurkundig

StromenIn Toestanden, natuurkundig is ruwweg één van de successen van de natuurkunde geschetst: hoe atomaire toestanden tot stand komen. Verzamelde fenomenologische kennis is gerubriceerd en gecombineerd met theoretische modellen tot er uiteindelijk een paar overbleven die de gevonden experimentele resultaten konden reproduceren en in staat bleken andere resultaten te voorspellen.

Hier wordt gewerkt aan het opstellen van de theorie van de menswetenschappen die ook echt "wetenschappen" genoemd kunnen worden, dat wil zeggen: ook werkelijkheden kunnen verklaren en voorspellen. Waaraan dus ook veel fenomenologisch werk vooraf zal moeten gaan. Wat hetgeen is waar hier mee gestart wordt.

Een eerste opmerking daarover is van algemenere aard: natuurkundigen hebben al opgemerkt dat het het makkelijkst is om eigenschappen van de natuur te meten als je dit doet in vergelijkende vorm: je vergelijkt twee dingen met elkaar en kijkt waarin ze verschillen en overeenkomen. Of: je kijkt naar een zaak en hoe deze in de tijd verandert. Dit is een voortzetting van wat de evolutie in de loop van haar bestaan heeft gedaan. Zo is het visuele waarnemingsstelsel is hoge mate toegespitst op intensiteitsverschillen, contouren, en met name bewegingen daarvan.

Ook in de eerste pogingen tot wetenschap is dat terug te zien: al uit de eerste tekenen van geschreven beschaving is duidelijk dat de vroege mens hevig geobsedeerd was door alle veranderingen en bewegingen in sterrenhemel: ten eerste de regelmatige waarvan we nu weten dat het komt door het ronddraaien van de aarde, en daar bovenop weer de bewegingen van planeten, kometen, enzovoort.

Het belang gehecht aan bewegingen en verandering strekt zich natuurlijk ook uit tot aardse verschijnselen. Makkelijk te bestuderen is de soort genaamd "stroming", omdat dit meestal langer duurt.

Ook met stromingen kan je toestanden associëren: de stroom gaat van een "hoge" toestand naar een "lage" toestand, zonder dat de toestanden zelf al te zeer veranderen door de stroming. Natuurkundigen noemen dit "quasi-stationaire" toestanden.

Het bekendste voorbeeld uit de menselijke leefwereld is de stroming van water, met name die tussen de quasi-stationaire toestanden van "gletsjer" en "oceaan" Info waterkringloop (afbeelding van hier uitleg of detail ):

De "toestand" is hier de hoogte van het waterpeil.

Voor natuurkundigen en overige mensheid veel interessanter is de stroming van warmte - in de natuurkunde bekend geworden als het vak der thermodynamica, voor de mensheid als de stoommachine en soortgelijke techniek. De "toestand" is hier de temperatuur, in stoommachines: die van het water annex stoom - warmte stroomt van hoge temperatuur, oftewel daar waar de deeltjes sneller botsen of trillen, naar lage (afbeelding van hier uitleg of detail ):

De regels hiervan zijn helaas wat minder inzichtelijk, vandaar dat we dit geval even verder laten liggen.

Een derde voorbeeld van stroming is dat van elektriciteit Info elektriciteit . Dat heeft als voordeel dat het makkelijk te meten is, zoals blijkt uit het redelijk vroege ontdekken (1827, qua publicatie) van de wet aangaande elektrische stroming: de wet van Ohm uitleg of detail . Die gaat over de elektrische stroom (letter \( I \), eenheid Ampère) in een draad wanneer er een spanning (spanning: letter \( V \), eenheid Volt) over staat - een bekend voorbeeld zijnde dat van de oude gloeilamp waar de bekende netspanning van 220 volt over staat en een zo sterke stroom door de draad gaat lopen dat ze heet wordt en gaat gloeien. De hoeveelheid stroom hangt ook af van de "weerstand" in de draad, met letter \( R \) en eenheid Ohm. Hoe meer weerstand, hoe minder stroom, en hoe meer spanning, hoe meer stroom. Tezamen:
\[ I ~ = ~ { { \Delta V } \over R } \]
De wet van Ohm ziet er dus simpel uit. Maar de natuurkunde erachter is dat niet. De stroom wordt gedragen door de losse elektronen in het metaal van de simpelste geleiders, zoals het wolfraam van de gloeidraad. Elektronen horen bij de atomen waaruit metaal en iedere stof bestaat, en van atomen bestaan er ten opzichte van onze zichtbare wereld altijd ontzettend veel. Natuurkundigen karakteriseren dat aantal met "het getal van Avogadro" uitleg of detail : \( 6 \times 10^{23} \) .

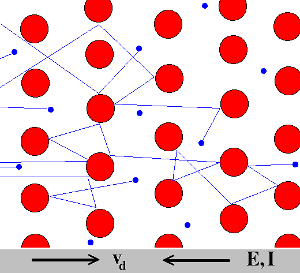
De elektronen in het metaal gaan steeds sneller door de spanning die over de draad staat, tot ze botsen met de atomen waar ze vanaf komen. En dan beginnen ze weer opnieuw met versnellen en sneller gaan. Tot ze weer botsen enzovoort:
Elektronen botsingen 

Het botsen van de elektronen doet de atomen trillen en maakt de draad heet en het zorgt uiteindelijk gemiddeld voor een constante stroom. Die constante stroom is de stroom die Ohm mat. De weerstand zorgt voor een contante stroom net als de luchtwrijving de auto een constante snelheid bezorgt ondanks het feit dat de motor voortdurend kracht erop uitoefent.

De wet van Ohm gaat dus over de beweging van ongeveer \( 6 \times 10^{23} \) elektronen, in plaats van bijvoorbeeld de beweging van één enkel gewicht zoals in het veer-experiment en de bijbehorende wet van Hooke, gebruikt als voorbeeld bij de afleiding van formules .

Door dat grote aantal, is de wet van Ohm niet wiskundig (analytisch) oplosbaar zoals de wet van Hooke, maar het is desondanks een geldige beschrijving.

Het geval van het stromen van water, weergegeven in de kop-illustratie, werkt identiek - de aandrijvende kracht is daar de zwaartekracht en de afremmende kracht komt van de botsingen met de bodem, oevers, rotsen, enzovoort.

Blijft nog de vraag wat in dit geval de toestand is. Dat zit verborgen in het gebruikelijke symbool voor de spanning, \( V \), wat eigenlijk \( \Delta V \) moet zijn, het verschil in potentiaal zoals spanning heet in de natuurkunde. De stroom loopt van hoge potentiaal naar lage potentiaal. Maar waar komt die potentiaal dan vandaan? Dat is de potentiaal waarmee de kernen trekken aan de geleidingselektronen in een metaal. Zoals boven. De geleidingelektronen zijn buitenste elektronen afkomstig van de atomen van het metaal, waardoor die atomen nu positief zijn. En de trekken aan de geleidingselektronen die negatief zijn. Waardoor het metaal één geheel blijft.

De elektrische kracht waarmee de kernen trekken aan de geleidingselektronen verschilt per metaal - de ene meer, de andere minder. Als je twee metalen op elkaar perst, worden de elektronen getrokken naar het metaal dat het hardste trekt. Er gaat dus een stroom lopen. De twee op elkaar geplakte metalen vormen samen een stroombron - een batterij. De spanning geleverd door de batterij als er geen stroom loopt, is die van het verschil van de twee aantrekkingskrachten binnen de metalen - bijvoorbeeld 1,86 volt voor zilver en zink en de bekende 1,5 volt voor de standaard koolstof-zink of alkaline batterij.

Merk hierbij op dat dit het resultaat is van alle atomen die allemaal elektronen afstaan, dus dat in feite de spanning is tussen ieder atoom en zijn geleidingselektronen als die uit de massa zou kunnen halen. Oftewel: die spanning is ook de spanning waarmee de kern aan de buitenste elektronen trekt. Oftewel: wat je ziet aan spanning van een batterij gaat regelrecht over de spanningen binnen de atomen. Oftewel: de spanning of potentiaal van batterijen is niet een alleen een macroscopisch gegeven, maar ook een microscopisch - het is een punt waar de werking van de microscopische, atomaire, wereld direct terug te zien is in de microscopische. Dit dus in tegenstelling tot eigenschappen als lading of massa, die je moet optellen. De macroscopische eenheidswaarde van lading, afgeleid uit direct meetbare eigenschappen, is 1 Coulomb, letter \( C \), en die van een elektron: \( 1,6 \times 10^{-19} C \) . De spanning waarmee het ene elektron vastzit binnen het waterstofatoom is 13,6 volt.


Dit wat betreft de natuurkunde als onderbouw voor de volgende stappen in de evolutie van de natuur, uitkomende bij de mens. Die evolutie vervolgt met de scheikunde , die de oneindigheid van combinaties an verschillende natuurkundige atomen behandelt.
    Wie direct naar menselijke toepassing wil: de sociologische toepassing van stroming start hier .


Naar Psychosociohistorie, inleiding , of site home ·.

17 jul.2015


De basis van het algemene verschijnsel van elektriciteit of elektromagnetisme is het specifieke verschijnsel van "lading" - iets dat je kan "maken" op diverse manieren waarvan redelijk bekend "de glazen staaf en kattenvel", of "synthetische stoffen en wrijven" in het algemeen, waarna al snel ontdekt werd dat dit een proces van "splitsing" veroorzaakt met de ene stof hebbende iets tegengestelds aan de andere waardoor de twee elkaar aantrokken - wat dus gedoopt is "lading", met de twee soorten als "plus"en min", waarbij de verkeerde is gekozen voor "plus", want degene die het meest beweegt, het veel lichtere elektron, is "min" en dat is lastig want die kan je dus het makkelijkste meten.
Ook de bronnen van rivieren, gletsjers, zouden miljoenen jaren geleden "op" zijn. De reden dat ze het niet zijn, is omdat ze constant aangevuld worden. Met oceaanwater. Dat eerst verdampt onder invloed van de zonnewarmte, opstijgt als waterdamp en wolken wordt, die landinwaarts drijven en daar verder opgestuwd worden, waarbij de waterdamp bevriest tot sneeuw. Die neerdaalt op de grotere hoogtes. Alwaar ze uitsneeuwen. En alle lagen sneeuw op elkaar worden gletsjers. Laat de aardetemperatuur een graad of zes dalen, en bijna heel Europa ligt onder de gletjers.