Formules, differentiaalvergelijkingenWie tot dit punt in de reeks over formules gekomen is, weet inmiddels dus wat formules zijn, en functies , en kan differentiëren
. En dat alles is hier
gepresenteerd als voortvloeiende uit de behoefte van de natuurkundige om
meer en preciezer te weten te komen wat er zoals gebeurt in de
(natuurkundige) wereld.Dat laatste kan ook gebruikt worden als inspiratiebron voor het ontwikkelen van differentiaalvergelijkingen. Het specifieke voorbeeld is dat wat er gebeurt met het rekken van een veer, als voorbeeld van het meer algemene geval van wat er kan gebeuren als je iets belast, zoals een stoomtrein over een stalen brug laten rijden. Het onderzoek van het rekken van een veer is, voor zover bekend, als eerste gedaan door de Engelsman Robert Hooke  . Wat hij bevond, en inmiddels
iedereen wel zo'n beetje weet, is dat als je een veer uitrekt, de kracht
toeneemt met de uitrekking:
\[ F ~ = ~ k \times \Delta l \]
Met \( \Delta l \) zijnde de verandering in lengte en \( k \) zijnde een
constante waarin de de stevigheid van de veer zit. Een "lineaire functie"
.
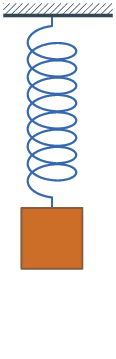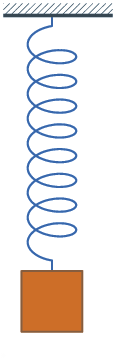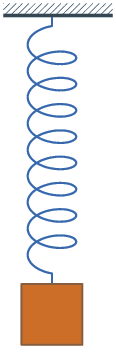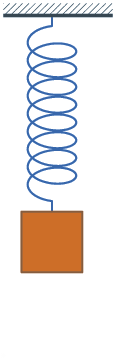 Waar hij niet aan toekwam, voor zover bekend, is de beschrijving van wat er gebeurt als je de
gerekte veer plotseling loslaat. Ook bijna iedereen weet wat er dan gebeurt:
het zaakje gaat op-en-neer bewegen, zie rechts. Maar waarom? En hoe zit die beweging in elkaar? Het antwoord daarop komt van de differentiaalvergelijking - zoals nu getoond gaat worden. En merk op: dit eerste stuk gaat niet over wiskunde maar natuurkunde, maar dit stuk behoort ook tot de fundamentele kennis die nodig is om een wetenschappelijke sociologie, een sociologie voorbij het niveau "botanie", te kunnen gaan bedrijven. De beweging die je ziet, is een verandering van plaats bij opeenvolgende tijden. Hetzelfde wat er gebeurt met een rijdende auto. Dit gaat dus over de grootheden \( x \) en \( t \) zoals beschreven in Formules, verschillen
. Wat toen wijselijk niet aan de orde is gekomen, is hoe de beweging tot
stand kwam - met zaken als "motoren" en "versnelling" en dergelijke.
Inmiddels is er genoeg gereedschap voorhanden om dat wel te kunnen doen.Dus terug naar de auto en beweging en dergelijke. De in Functies, grafieken
getoonde grafiek voor de plaats van de auto versus de tijd was geen rechte
lijn. Dat is logisch, want een rechte lijn, weten we inmiddels, staat voor
een constante snelheid. En een auto heeft niet zomaar een constante
snelheid, en als hij zomaar een constante snelheid heeft, is deze nul - hij
staat geparkeerd voor de deur. Om hem een echte snelheid te geven moet de
motor gestart worden en gasgegeven, dat wil zeggen: er moet energie in. Door
die energie krijgt de auto snelheid. Als je, eenmaal op de snelweg, het gas
loslaat, blijft hij in principe gewoon doorrijden. Dat het in de praktijk
niet gebeurt, komt door, weet inmiddels ook iedereen, de wrijving. Maak de
wrijving klein, en de auto blijft langer doorrijden. Maak de wrijving nul,
en de auto blijft eeuwig doorrijden. Dat doet de maan ook, in zijn baan om
de Aarde.Dus de energie van de benzine gaat niet in de snelheid. Direct. Die energie gaat in de versnelling - het op snelheid komen. En door het op snelheid komen, is er ook snelheid. Die, als je voortdurend dezelfde hoeveelheid energie in blijft stoppen, ook voortdurende toeneemt. Afgezien weer van die wrijving. Allemaal topnatuurkunde. Voor de zeventiende eeuw. Die Hooke nog niet (voldoende) had. Wat Hooke wél had, was het begrip "kracht", als afkorting van de moeite die ergens ingestopt moest worden om het te veranderen, zoals dus het langer maken van zijn veer. En bij de veer heb je maken met minstens twee krachten: die van de veer, vanzelfsprekend, en de zwaartekracht - die aan de veer naar beneden trekt. En hangende stil, trekt de veerkracht dus naar boven. Even sterk. Daarna gaat de mens er nog eens aan trekken, en komt het zaakje lager te hangen. Laat het dan los, en het wiebelen van de illustratie begint. Met dus een versnelling, net als bij de auto, want de snelheid was eerste nul en neemt daarna toe. Dus als eerste stap heb je nodig de kennis hoe het zit met kracht en versnelling. Die kennis komt van de "opvolger" van Hooke": Newton . Zijn observatie luidde: kracht is massa maal versnelling. En
toen het afkorten geleend van de wiskundigen ingeburgerd raakte:
Maar dan rest er nog een tweede: Hoe zit het met versnelling en snelheid? Gelukkig is die vraag qua methodiek al beantwoord. Het methodiek-antwoord luidt: op dezelfde manier als tussen snelheid en plaats. Waar snelheid de verandering van plaats per tijdseenheid is:
Hooke had dus zelf het antwoord gevonden hoe het met de kracht en de eigenschappen van de veer zit, en nu weten we hoe het zit met kracht en beweging. Die zaken kunnen we dus combineren. Waarvan de eerste stap is alles in dezelfde richting te bekijken, waarvoor we, hoewel het spel zich vertikaal afspeelt, toch maar de aanduiding \( x \)-richting gebruiken. Dus neem eerst de wet van Hooke zoals eerst geformuleerd:
Of in vollediger wiskunde-termen: "een tweede-orde differentaalvergelijking in \( x \) als functie van \( t \)". En deze specifieke differentiaalvergelijking kan je ook beschrijven in gewonere taal: Als de plaats een functie van de tijd is: \( x(t) \) , en je neemt het geval van de plaats van een gewicht hangende aan een veertje, en je differentieert die functie van plaats naar tijd twee keer achter elkaar, dan krijg je de oorspronkelijke plaatsfunctie terug, zij het vermenigvuldigt met een bepaalde factor. En die factor hangt af van de massa van het gewicht en de stevigheid, rekbaarheid, van de veer. En na al dit heen-en-weer geschuif even een gesimplificeerde samenvatting - neem de wet van Hooke in de \(x\)-richting:
Bij gebrek aan wiskundigen in deze contreien, doen we zelf een poging hier  . Naar Evolutie 
, of
site home
 .
|