Formalisme: toestanden, natuurkundig
 Van
het programma van het overbrengen van de methodieken van de
natuurwetenschappen naar de menswetenschappen is een eerste deel (voorlopig)
afgehandeld: het aanbrengen van structuren in het onderzoeksveld. De tweede
stap na het splitsen in onderzoeksvelden zelf. En onderweg zijn al een
aantal ruwe of globale karakteristieken van die structuren gegeven. Van
het programma van het overbrengen van de methodieken van de
natuurwetenschappen naar de menswetenschappen is een eerste deel (voorlopig)
afgehandeld: het aanbrengen van structuren in het onderzoeksveld. De tweede
stap na het splitsen in onderzoeksvelden zelf. En onderweg zijn al een
aantal ruwe of globale karakteristieken van die structuren gegeven.
De natuurkunde is al een stap verder: die is in staat om de deelstructuren
te beschrijven tot het niveau waar voorspellingen mogelijk zijn, en die te
testen. Waarmee de cirkel tot stand is gekomen die de vooruitgang ervan
gebracht heeft
 . .
Hier wordt als voorbeeld een van de succesvolle
beschrijving van deelstructuren samengevat, die van het atoom.
Het
atoom was al afgebeeld in Generalisaties, natuurlijk
 als een soort planetenstelsel (eigenlijk moet je de elektronenbanen in eigen
vlakken tekenen zodat het al meer lijkt op de bol zoals het zich daadwerkelijk
gedraagt):
als een soort planetenstelsel (eigenlijk moet je de elektronenbanen in eigen
vlakken tekenen zodat het al meer lijkt op de bol zoals het zich daadwerkelijk
gedraagt):
Waarbij al gesteld is dat dat zou moeten leiden tot het uitzenden van
licht en andere soort elektromagnetische straling waardoor het
elektron steeds lager zou gaan draaien en uiteindelijk in de kern storten.
Als je dat licht dan gaat splitsen in zijn kleuren, bijvoorbeeld met
een prisma, krijg je een spectrum als dat van de regenboog:
Wat je werkelijk ziet als je atomen als gas verhit of anderszins energie in
stopt, bijvoorbeeld in een tl-buis of een xenon-lamp van een auto, is dit:
Oftewel: elektronen die in losse atomen zitten, zenden alleen licht uit van zeer specifieke kleuren,
dat wel zeggen: gaan op en neer tussen zeer specifieke energietoestanden.
Toen natuurkundigen dat ontdekten, en er waren zeer veel van dit soort
spectra, wilden ze er natuurlijk achter komen hoe dat kwam - die zeer specifieke
energietoestanden.
Daarvoor moeten ze eerste twee dingen doen: die spectra sorteren en
rubriceren. En bij een bepaald soort rubricering, bleken er ook redelijk
klinkende verklaringen gevonden te kunnen worden. En één van die redelijk
klinkende verklaringen bleek ook te passen bij andere inzichten en
verklaringen en ook weer nieuwe inzichten en verklaringen te verschaffen.
De verklaring dat deeltjes zoals elektronen naast massa ook een
golfverschijnsel kennen, onder de naam "quantummechanica", dat indien
opgesloten in een atomaire baan, leidt tot zeer specifieke toestanden zoals
de zeer specifieke noten van een trommelvel:
Bij de combinatie van elektromagnetische en quantummechanische
interactie werd in 1927 een wiskundige vergelijking gevonden door Erwin
Schrödinger
 , die er zo uitziet: , die er zo uitziet:
|
\[ { - \hbar^2 \over {2m} } {\partial^2 \Psi \over {\partial x}^2} ~
+ ~ V(x)\, \Psi ~ = ~ {i \hbar} {\partial \Psi \over {\partial t}} \]
|
Waarin \( \Psi \) staat voor het golfverschijnsel, \( V(x) \) staat voor
de elektrische spanning, \( \hbar \) voor de constante van Planck die
golfverschijnsel aan massa koppelt.
En voor stabiele toestanden (met
constante energie) wordt dit:
|
\[ { - \hbar^2 \over {2m} }
{\partial^2 \Psi \over {\partial x}^2} ~ + ~ V(x)\, \Psi ~
= ~ E \Psi \]
|
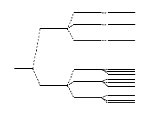
Deze vergelijkingen gaan we hier niet oplossen - we geven alleen de
resultaten. En niet eens de hele vorm van die resultaten, maar slechts één
eigenschap er van: het is er een hele reeks van die slechts verschillen in
een geheel getal volgens de reeks 1, 2, 3, enzovoort. Ieder met een eigen
energie. Iets dat men gewoonlijk zo grafisch uitbeeldt:
Het bovenstaande is een speciaal en simpel en geval. Voor het meer algemene geval zijn er
nog twee andere getallen die de toestand karakteriseren, die te maken hebben
met de hoeveelheid rotatie van de baan rond de kern
("omwentelingsnelheid"), met de letters "\(l\)" en "\(m\)" . En eentje met de rotatie
van het elektron zelf met letter "\(s\)" van "spin", het Engelse
woord voor "rondtollen".
De discrete spectrum
ontstaat
door overgangen van de elektronen tussen de atomaire niveaus. Omhoog
bijvoorbeeld door botsing met een ander atoom (door de hitte van het gas),
en omlaag gepaard gaande met het uitzenden van licht, weergegeven met pijlen
in de spectra:
Direct na het leren van het voorgaande, krijgen natuurkundestudenten (en
scheikunde-) nog een cruciaal begrip voorgeschoteld, dat van de
"selectieregels". Want zodra je uit het spectrum de ladder van toestanden
hebt gereconstrueerd, blijken bepaalde overgangen tussen de niveaus niet
voor te komen. Dat geldt met name voor het rotatiequantunmgetal met letter
"\(l\)" en de totale rotatie \( J = \, l \,+\,s \) . Een overgang tussen toestanden met verschillende rotatiequantumgetal
betekent dat de toestand van het atoom waar het om gaat "minder snel om zijn
as gaat draaien". Dat kan niet, in de natuur. De hoeveelheid rotatie moet
altijd hetzelfde blijven. Maar het licht dat uitzonden wordt bij een
overgang, heeft ook een hoeveelheid rotatie. het atoom kan slecht zo veel in
rotatie veranderen als het licht meeneemt. En dat laatste is een vaste
waarde. En de toestand kan dus alleen veranderen met die vaste waarde. En
als je die vaste waarde voor het gemak even op 1 stelt, verandert de
rotatietoestand dus altijd met 1 - omhoog of omlaag, dus ±1 - te lezen als:
"plus of minus één"- en dus niet als "ongeveer één".
Vandaar dat in
het laatste energieschema alleen de getekende pijlen voorkomen, en niet
degene die twee of meer stappen nemen.
Dit is dus hoe de natuurkunde
het probleem van "Hoe zit een atoom in elkaar?" heeft opgelost. Het werkt
alleen exact voor het simpelste atoom: waterstof. Voor grotere atomen heeft
men handige benaderingstrucs bedacht. Net als voor moleculen. En bij andere
zaken past men weer andere trucs en benaderingen toe. Maar de basale
werkwijze is hetzelfde: ga uit van wat elders wel heeft gewerkt, probeer
wat, kijk of het werkt, en zo nee, probeer wat anders
 . .
Dit is het voorbeeld dat
andere wetenschappen wordt voorgehouden. Exactheid, zoals gesuggereerd in de
zeer foutieve naam "exacte wetenschappen", is geen vereiste. Wel:
objectiviteit.
Uit de biologie hebben we bij Generalisaties,
natuurlijk
 al voorbeelden gezien van toestanden met weinig aanverwante
toestanden om zich heen, onder de noemer "structuren". Die dus veel
weg hebben van moeilijk veranderbare toestanden, oftewel: min-of-meer
discrete toestanden. In de psychologie en sociologie zijn ook voorbeelden
aan te wijzen - in de
psychologie: het veranderen van religieus zijn
al voorbeelden gezien van toestanden met weinig aanverwante
toestanden om zich heen, onder de noemer "structuren". Die dus veel
weg hebben van moeilijk veranderbare toestanden, oftewel: min-of-meer
discrete toestanden. In de psychologie en sociologie zijn ook voorbeelden
aan te wijzen - in de
psychologie: het veranderen van religieus zijn
 . In de sociologie: het veranderen van cultuur
. In de sociologie: het veranderen van cultuur
 .
.
In de sociologie zijn zelfs voorbeelden te vinden van een van de
regels afgeleid van het bestaan van min-of-meer discrete toestanden: de
selectieregels. Hier is een afbeelding een van de eerste
auto's:
Het is een koets met het paard vervangen door een motor. Het duurde weer iets als een halve generatie voordat de moderne auto
ontstond. En er zijn veel meer van dit soort voorbeelden uit de techniek.
Waarbij ook voor de sociologie lijkt te gelden dat geleidelijke
veranderingen met slechts met één stap tegelijk gaan. Met meer drastische
veranderingen voorbehouden aan "revolutie"
 . .
Het was al duidelijk dat er meer dan genoeg aanwijzingen dat er ook in de sociologie gelaagde
structuren zijn te vinden. Nu is daar dus bij gekomen dat dat ook geldt voor
het meer gedetailleerde begrip van toestanden. Dat maakt dat wat hier
aanvankelijk een aanname was: dat er ook binnen de sociologie gewerkt kan worden
met de methoden van de natuurkunde, gewoon ook op praktische gronden zeer
plausibel. Een idee dat in de meer tot "rekenen" geneigde economie en met name
de econometrie wel is doorgedrongen, gezien deze presentatie van een
econometrische formule:
Zoals uitgebreid uitgelegd in Formules, differentiaalvergelijkingen,
toepassingen
 , gaat deze formule over de verandering van een raamwerkfunctie \( \chi \),
terwijl de Schrödinger-vergelijking gaat over de veranderingen van een
raamwerkfunctie \( \Psi \) . In de econometrie-formule in combinatie met de
parameter \( T \) en \( W \) staande voor "taxation" en "wealth",
in de Schrödinger-vergelijking in combinatie met de parameters \( V \) en \( E
\) staande voor elektrische potentiaal en energie.
, gaat deze formule over de verandering van een raamwerkfunctie \( \chi \),
terwijl de Schrödinger-vergelijking gaat over de veranderingen van een
raamwerkfunctie \( \Psi \) . In de econometrie-formule in combinatie met de
parameter \( T \) en \( W \) staande voor "taxation" en "wealth",
in de Schrödinger-vergelijking in combinatie met de parameters \( V \) en \( E
\) staande voor elektrische potentiaal en energie.
Waar de aanpak dus werkt voor de natuurkunde en de econometrie, is het dus
vrijwel zeker dat ze ook kan werken voor het tussenliggende gebied van de
sociologie. Met dus meteen een suggestie voor de betekenis van de
raamwerkfunctie binnen de sociologie. Want binnen de natuurkunde stelt men
gewoonlijk dat met de functie wel rekening gehouden moet worden in verband
met zijn representatie van het golfverschijnsel, maar zelf geen betekenis heeft
indien losstaand. Maar wel indien met zichzelf vermenigvuldigd oftewel de
intensiteit of absolute waarde ervan - die betekenis is de deeltjes- of
toestandsdichtheid of de kans, letter \( P \) , om een deeltje of toestand te
vinden of waar te nemen:
|
\[ P ~ = ~ \Psi^* \Psi \]
|
Met de "*" zijnde het symbool voor complex conjugeren, zie Formules, complexe
getallen
 .
.
De vertaling naar sociologie ligt dan bijna voor de hand: daar heeft het
kwadraat van de raamfunctie dan de betekenis van de kans om een individu in
een bepaalde toestand aan te treffen oftewel binnen een bepaalde groep dat
deel ervan dat een bepaalde eigenschap heeft.
Hoe nu verder met dit
doel voor de sociologie? Het punt waarop de Schrödinger-vergelijking werd
ontdekt en bijna tegelijkertijd een soortgelijke methodiek door Werner
Heisenberg
 , was het eindpunt van een ontwikkeling die startte rond de
16de en 17de eeuw met mensen als Galileo, Huygens en Newton met vooral veel
vooruitgang op het veld van de bestudering van natuurlijke verschijnselen -
de fenomenologie. De combinatie hiervan met de theorie leverde de moderne
wetenschap op , was het eindpunt van een ontwikkeling die startte rond de
16de en 17de eeuw met mensen als Galileo, Huygens en Newton met vooral veel
vooruitgang op het veld van de bestudering van natuurlijke verschijnselen -
de fenomenologie. De combinatie hiervan met de theorie leverde de moderne
wetenschap op
 .
.
Het ligt voor de hand om dit ook voor de sociologie op deze manier te doen.
Dus met eerst veel aandacht voor de fenomenologie. Startende met "stromen"
 . .
Naar Psychosociohistorie, inleiding
 ,
of site home ,
of site home
 ·. ·.
|